
FEMAP V10.1 & NX Nastran 6.1 Tutorial
Análisis de Frecuencias del Chasis de un Vehículo
(Septiembre, 2009)
El objetivo de este Tutorial es aprender a calcular las frecuencias de resonancia hasta un valor de 50 Hz usando el Método de Lanczos. También aprenderemos a incluir en el cálculo la obtención de la energía de deformación en un grupo de elmentos para ayudar a caracterizar los modos de vibración resultantes. Y por último se pedirá el cálculo de las matrices de masa de cuerpo rígido a través de la entrada "PARAM,GRDPNT,0".
Si quieres repetir este tutorial en tu propio ordenador pídenos los modelos con la geometría de entrada y te lo remitimos por e-mail, es un servicio gratuito para nuestros clientes.
![]() 1. Descripción del Problema
1. Descripción del Problema
La siguiente imagen muestra el modelo de Elementos Finitos del
chasis de aluminio de un vehículo. El modelo está compuesto por elementos
Shell (CQUAD4 y CTRIA3) y muelles (CELAS2) representando la suspensión. La
rigidez de la suspensión se mete a través de los muelles en las tres
direcciones de translación: rigidez KY=500 lb/in en la dirección vertical y
KX=KZ=1000 lb/in en las otras dos direcciones.
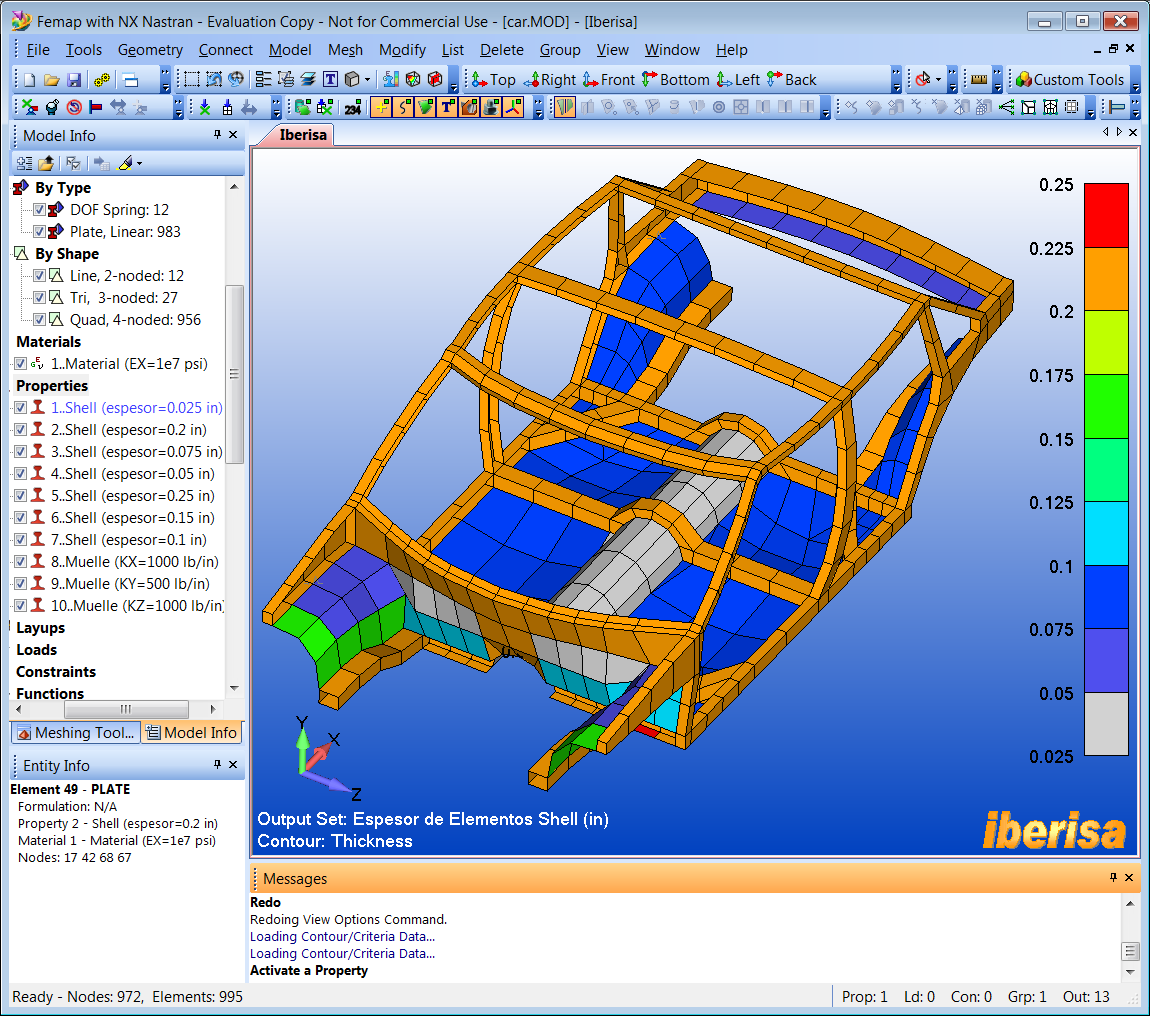
Modelo del Chasis del Vehículo mallado con elementos
CQUAD4 y CTRIA3
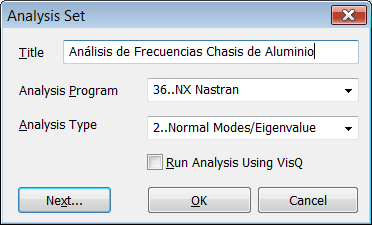
q 2.1. Definición del Tipo de Análisis
Desde "Model > Analysis" definimos los parámetros del análisis dinámico de frecuencias (SOL103) con el solver NX Nastran.
q
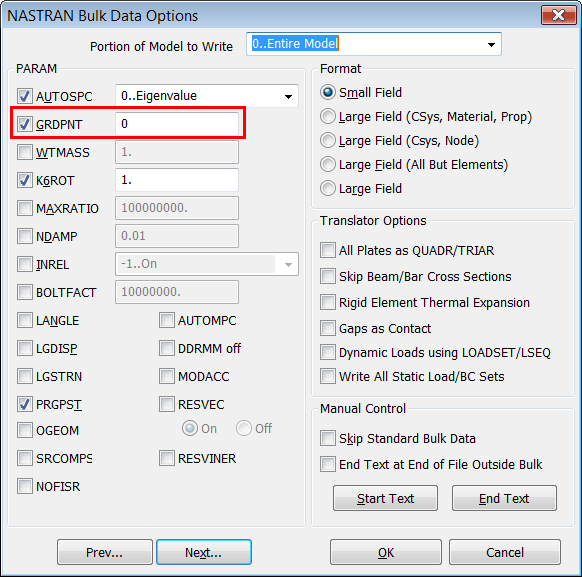
2.2.
Escritura
de las Matrices de Masa de Cuerpo Rígido
Para que el solver NX Nastran escriba en el
fichero *.F06 las matrices de masa de cuerpo rígido se debe activar la entrada
"PARAM,GRDPNT,0" en la siguiente ventana:
q
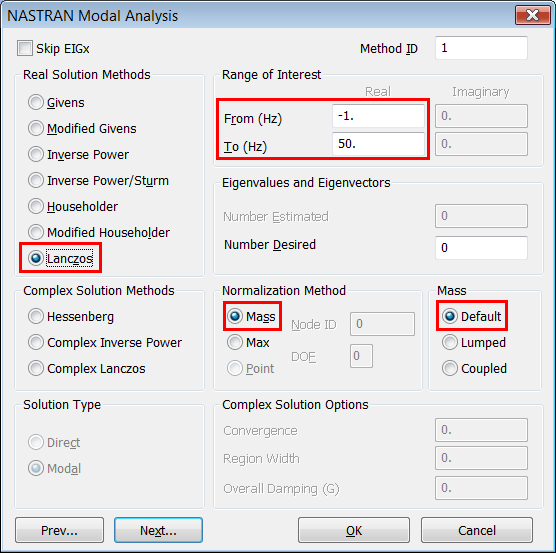
2.3.
Parámetros de NX
Nastran para el Análisis Modal
En el campo "Range of Interest"
se introducen los valores -1 y 50 para solicitar al solver NX Nastran que
obtenga todos los modos propios del modelo por debajo de los 50 Hz utilizando el
Método de Lanczos:
q
2.4.
Petición de
Resultados
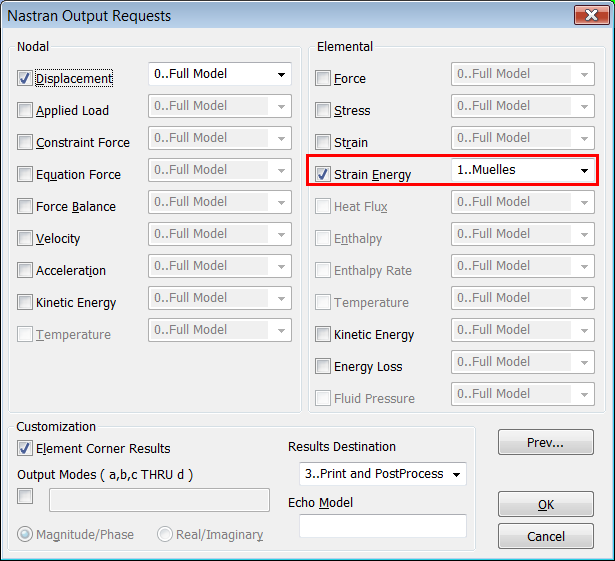
Se crea un grupo con los elementos muelle del
modelo y se solicita al solver NX Nastran el cálculo de la Energía de
Deformación en esos elementos:
![]() 3. Postprocesado de los Resultados del Análisis
3. Postprocesado de los Resultados del Análisis
q
3.1.
Resultados del fichero
*.F06
El resultado "grid point weight
generator" indica que la masa translacional del modelo tiene un valor
de 0.8027 lb-sec2/in. Ese tipo de información es
muy útil a la hora de verificar el modelo. El resultado "eigenvalue
analysis summary" indica que hay 12 modos por debajo de los 50 Hz. El
valor elevado de la energía de deformación en elementos muelle en los seis
primeros modos de vibración indica que esos son los modos primarios de la
suspensión, con el chasis del vehículo actuando como un cuerpo rígido
soportado por muellos flexibles. Aproximadamente el 95% de la energía total de
deformación está representada por la deformación de los muelles en oposición
a la deformación del chasis. El Modo#7 y posteriores muestran una energía de
deformación insignificante, indicando que esos son los modos primarios del
chasis.
* * * * * * * * * * * * * * * * * * * *
* * * * * * * * * * * * * * * * * * * *
* * * *
* * * *
* * * *
* * * *
* * N X N a s t r a n * *
* * * *
* * VERSION - 6.1 * *
* * * *
* * JAN 19, 2009 * *
* * * *
* * * *
* *Intel64 Family 6 Model 23 Steppi * *
* * * *
* *Intel(R) Core(TM)2 Quad CPU Q955 * *
* * * *
* * Windows Vista * *
* * * *
* * Compiled for X86-64 * *
* * * *
* * * * * * * * * * * * * * * * * * * *
* * * * * * * * * * * * * * * * * * * *
M O D E L S U M M A R Y
NUMBER OF GRID POINTS = 972
NUMBER OF CELAS2 ELEMENTS = 12
NUMBER OF CQUAD4 ELEMENTS = 956
NUMBER OF CTRIA3 ELEMENTS = 27
O U T P U T F R O M G R I D P O I N T W E I G H T G E N E R A T O R
0 REFERENCE POINT = 0
M O
* 8.027377E-01 0.000000E+00 0.000000E+00 0.000000E+00 -2.808118E+01 -2.179473E+01 *
* 0.000000E+00 8.027377E-01 0.000000E+00 2.808118E+01 0.000000E+00 7.610538E+01 *
* 0.000000E+00 0.000000E+00 8.027377E-01 2.179473E+01 -7.610538E+01 0.000000E+00 *
* 0.000000E+00 2.808118E+01 2.179473E+01 2.325008E+03 -2.153941E+03 2.662697E+03 *
* -2.808118E+01 0.000000E+00 -7.610538E+01 -2.153941E+03 1.020871E+04 7.626399E+02 *
* -2.179473E+01 7.610538E+01 0.000000E+00 2.662697E+03 7.626399E+02 9.437678E+03 *
S
* 1.000000E+00 0.000000E+00 0.000000E+00 *
* 0.000000E+00 1.000000E+00 0.000000E+00 *
* 0.000000E+00 0.000000E+00 1.000000E+00 *
DIRECTION
MASS AXIS SYSTEM (S) MASS X-C.G. Y-C.G. Z-C.G.
X 8.027377E-01 0.000000E+00 2.715050E+01 -3.498177E+01
Y 8.027377E-01 9.480729E+01 0.000000E+00 -3.498177E+01
Z 8.027377E-01 9.480729E+01 2.715050E+01 0.000000E+00
I(S)
* 7.509410E+02 8.764164E+01 -3.961892E-01 *
* 8.764164E+01 2.011030E+03 -2.217122E-01 *
* -3.961892E-01 -2.217122E-01 1.630594E+03 *
I(Q)
* 2.017097E+03 *
* 7.448744E+02 *
* 1.630595E+03 *
Q
* 6.905322E-02 9.976128E-01 4.970477E-04 *
* -9.976128E-01 6.905345E-02 -4.682789E-04 *
* -5.014840E-04 -4.635249E-04 9.999998E-01 *
E I G E N V A L U E A N A L Y S I S S U M M A R Y (READ MODULE)
BLOCK SIZE USED ...................... 7
NUMBER OF DECOMPOSITIONS ............. 3
NUMBER OF ROOTS FOUND ................ 12
NUMBER OF SOLVES REQUIRED ............ 11
R E A L E I G E N V A L U E S
MODE EXTRACTION EIGENVALUE RADIANS CYCLES GENERALIZED GENERALIZED
NO. ORDER MASS STIFFNESS
1 1 2.339853E+03 4.837202E+01 7.698647E+00 1.000000E+00 2.339853E+03
2 2 2.648059E+03 5.145929E+01 8.190001E+00 1.000000E+00 2.648059E+03
3 3 3.762816E+03 6.134180E+01 9.762850E+00 1.000000E+00 3.762816E+03
4 4 4.588920E+03 6.774157E+01 1.078141E+01 1.000000E+00 4.588920E+03
5 5 5.067349E+03 7.118532E+01 1.132949E+01 1.000000E+00 5.067349E+03
6 6 8.458979E+03 9.197271E+01 1.463791E+01 1.000000E+00 8.458979E+03
7 7 2.672128E+04 1.634664E+02 2.601649E+01 1.000000E+00 2.672128E+04
8 8 4.843912E+04 2.200889E+02 3.502824E+01 1.000000E+00 4.843912E+04
9 9 5.396764E+04 2.323094E+02 3.697318E+01 1.000000E+00 5.396764E+04
10 10 8.438609E+04 2.904929E+02 4.623337E+01 1.000000E+00 8.438609E+04
11 11 9.051163E+04 3.008515E+02 4.788200E+01 1.000000E+00 9.051163E+04
12 12 9.520502E+04 3.085531E+02 4.910775E+01 1.000000E+00 9.520502E+04 E L E M E N T S T R A I N E N E R G I E S
ELEMENT-TYPE = ELAS2 * TOTAL ENERGY OF ALL ELEMENTS IN PROBLEM = 1.169926E+03
MODE 1 * TOTAL ENERGY OF ALL ELEMENTS IN SET 1 = 1.098327E+030
ELEMENT-ID STRAIN-ENERGY PERCENT OF TOTAL STRAIN-ENERGY-DENSITY
1002 2.713274E+02 23.1918
1003 5.206163E-02 0.0044
1012 2.664482E+02 22.7748
1013 4.285339E-02 0.0037
1021 9.543382E-02 0.0082
1022 2.823194E+02 24.1314
1023 4.207681E-01 0.0360
1031 9.413449E-02 0.0080
1032 2.771417E+02 23.6888
1033 3.810864E-01 0.0326
TYPE = ELAS2 SUBTOTAL 1.098327E+03 93.8800
../..
E L E M E N T S T R A I N E N E R G I E S
ELEMENT-TYPE = ELAS2 * TOTAL ENERGY OF ALL ELEMENTS IN PROBLEM = 1.336064E+04
MODE 7 * TOTAL ENERGY OF ALL ELEMENTS IN SET 1 = 3.190767E+030
ELEMENT-ID STRAIN-ENERGY PERCENT OF TOTAL STRAIN-ENERGY-DENSITY
1001 1.271633E+02 0.9518
1002 5.888319E+02 4.4072
1003 8.088802E+01 0.6054
1011 1.271580E+02 0.9517
1012 5.887681E+02 4.4067
1013 8.090958E+01 0.6056
1021 7.315770E+01 0.5476
1022 4.866266E+02 3.6422
1023 2.381976E+02 1.7828
1031 7.317775E+01 0.5477
1032 4.876783E+02 3.6501
1033 2.382102E+02 1.7829
TYPE = ELAS2 SUBTOTAL 3.190767E+03 23.8818 |
q
3.2.
Modos de Vibración
El Modo#7 es un modo de torsión general. El
Modo#8 es un modo de "colapso del techo", el Modo#9 es un modo local
(frontal) del techo, y el Modo#10 es un modo local trasero. La animación de la
deformada de los diferentes modos de vibración junto con los valores de
energía de
deformación en los muelles ayuda a ilustrar cada uno de los modos de
vibración del chasis.
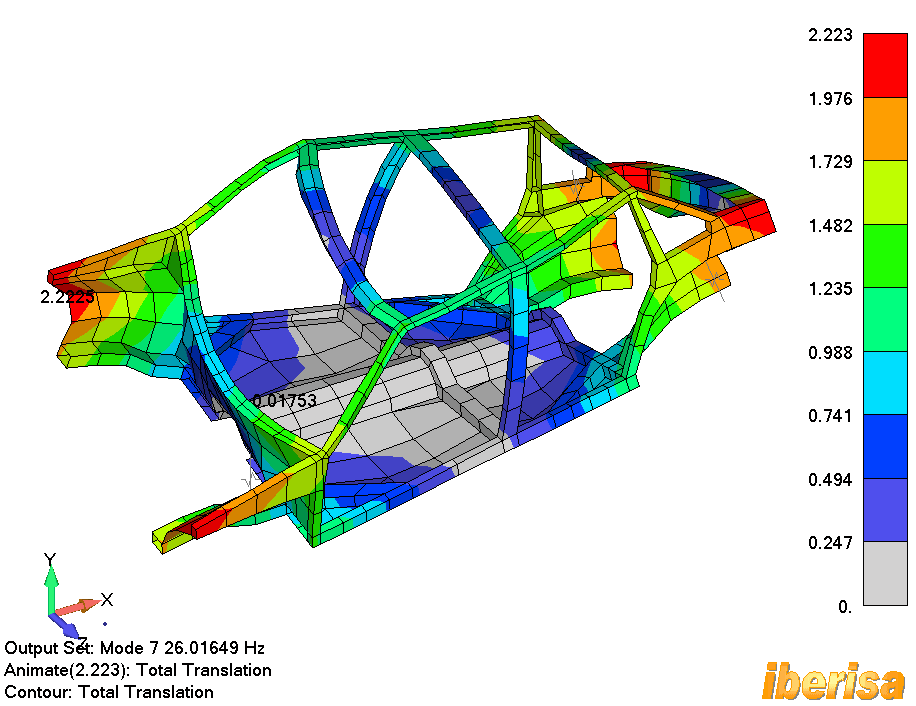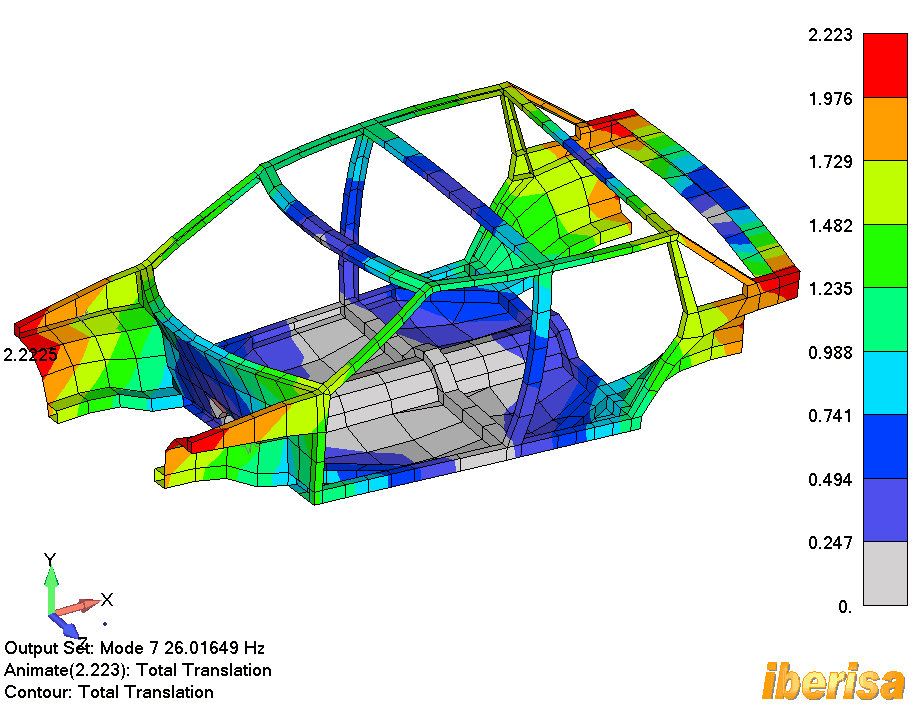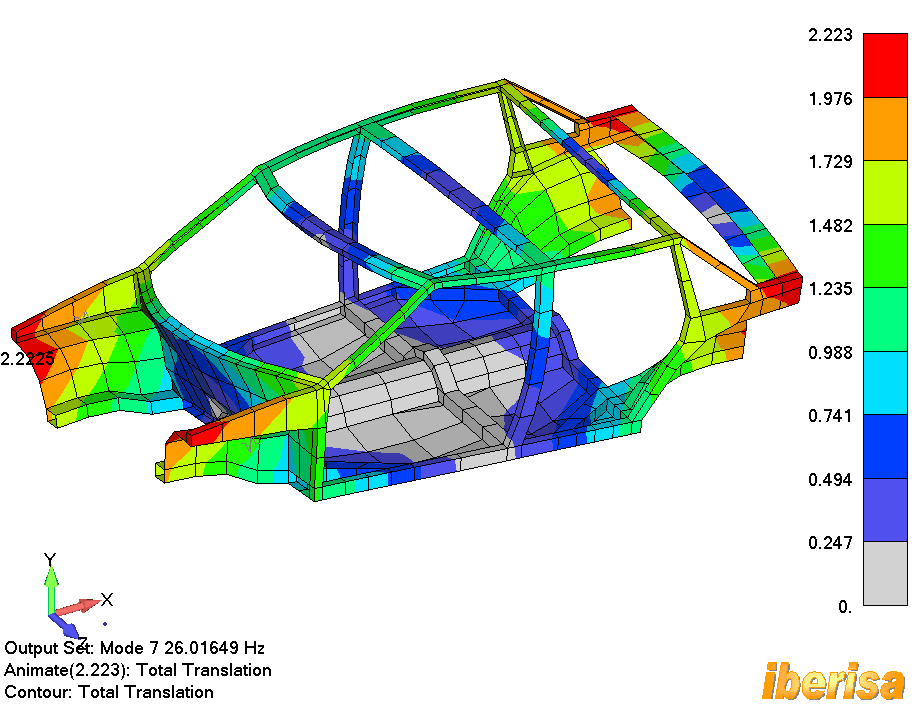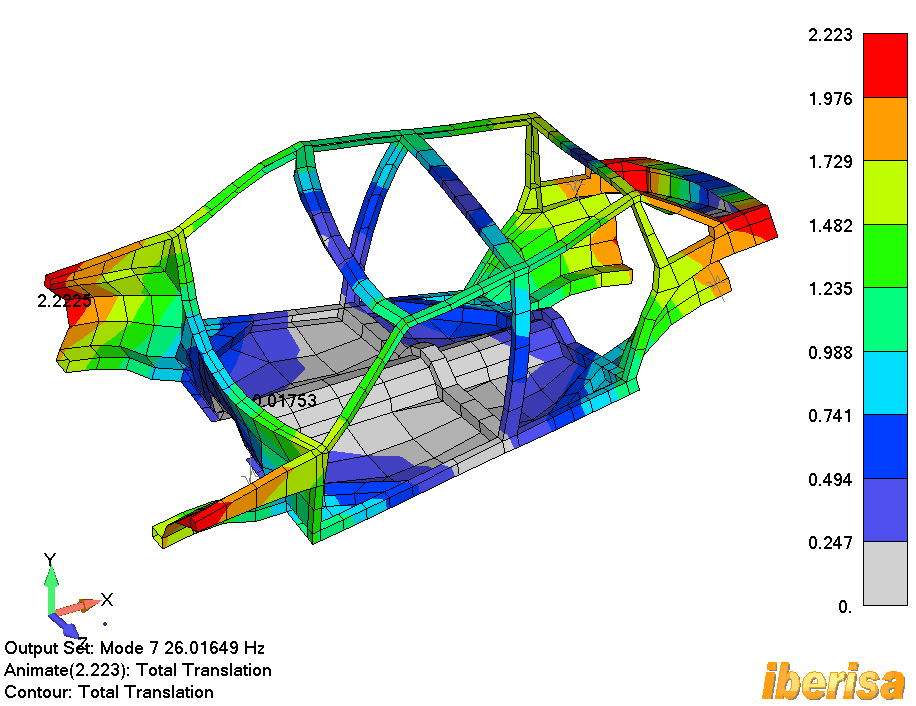
Modo#7: Modo de Torsión General
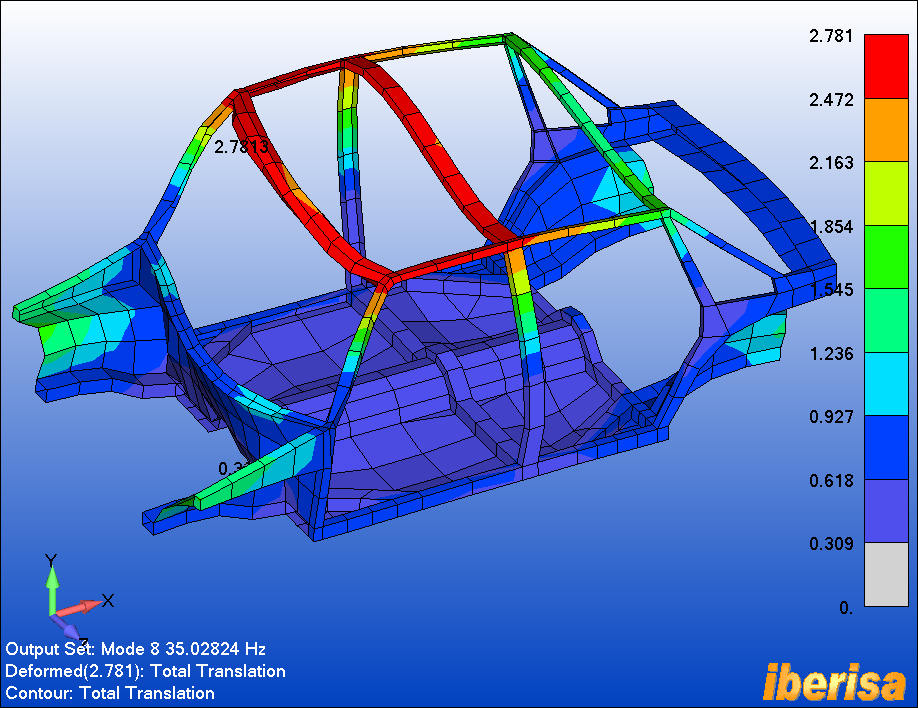
Modo#8: Modo de Colapso del Techo
del Vehículo
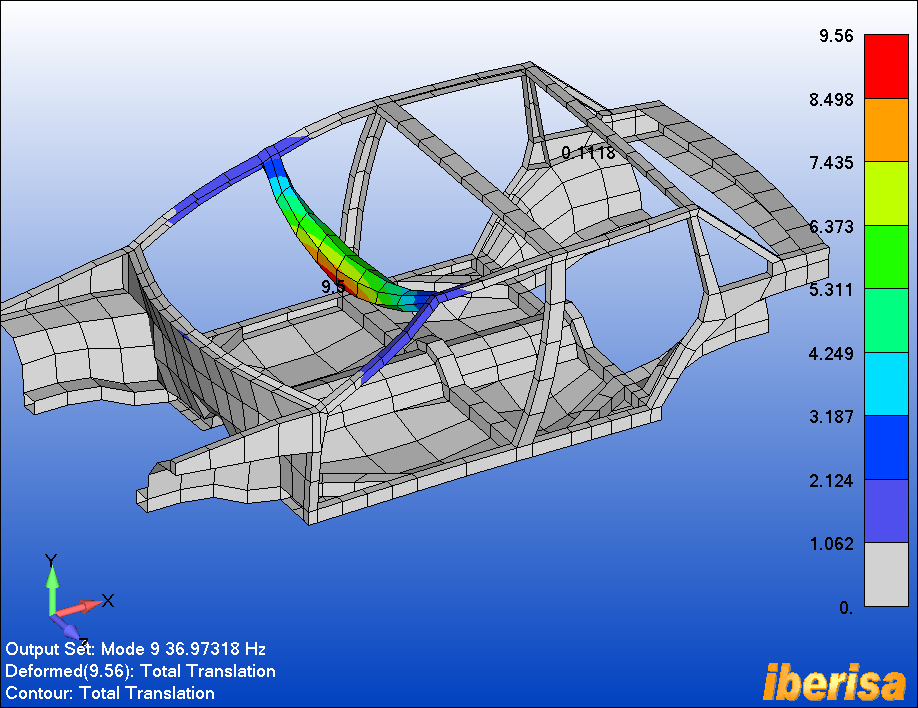
Modo#9: Modo Local (frontal) del
Techo
Espero que el tutorial os haya resultado útil e interesante!!.
Saludos,
Blas.
