FEMAP V10.1.1 & NX Nastran 7.0 Tutorial
Unión mediante soldaduras Punto-a-Punto
Análisis No Lineal Estático (2ª Parte)
(Marzo, 2010)
En la 1ª Parte nos dimos cuenta que los desplazamientos resultantes del análisis estático lineal del modelo de elementos finitos eran tan elevados que se hacía necesario contrastar la solución lineal (SOL101) mediante un análisis no lineal por la geometría (SOL106) activando la opción de "Large Displacements". Pues bien, en este tutorial os enseño cómo resolver el modelo de elementos finitos como No Lineal por la Geometría con los programas FEMAP & NX NASTRAN y comparar resultados lineales y no lineales, incluyendo una explicación del comportamiento del modelo.
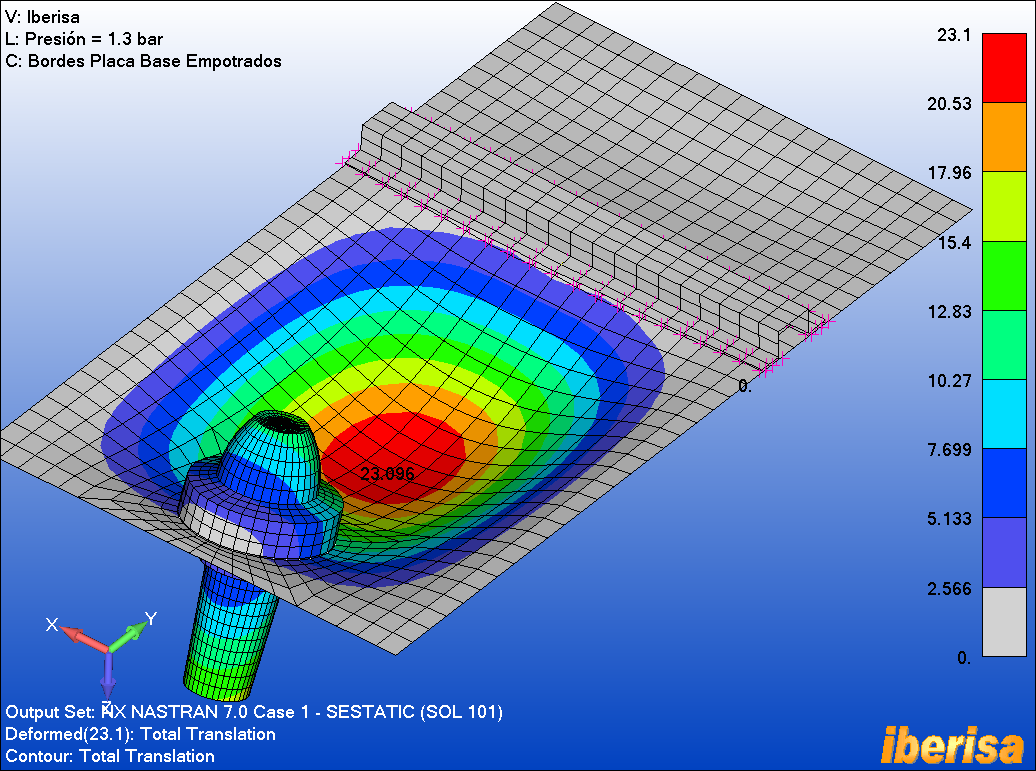
Resultados de desplazamientos (mm) del
Análisis Estático Lineal (SESTATIC SOL101)
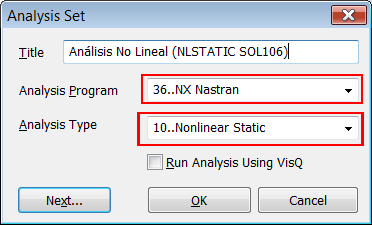
1. Definición del Análisis Estático No Lineal (NLSTATIC SOL106)
En "Model > Analysis > New"
definimos el análisis estático no lineal utilizando el solver NX NASTRAN 7.0:
 |
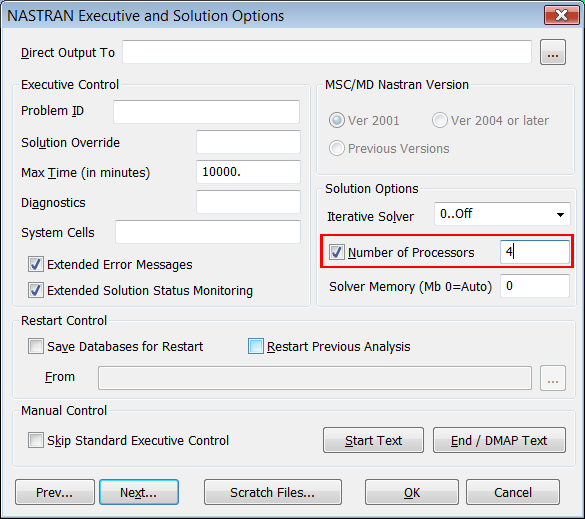
En "NASTRAN Executive and Solution Options" recomiendo activar el número de procesadores presentes en tu ordenador, de esta forma NX NASTRAN aprovecha todas las CPUs disponibles y acelera de forma notable el proceso de cálculo, muy importante en el caso de realizar análisis no lineales donde el tiempo de solución es importante: |
|
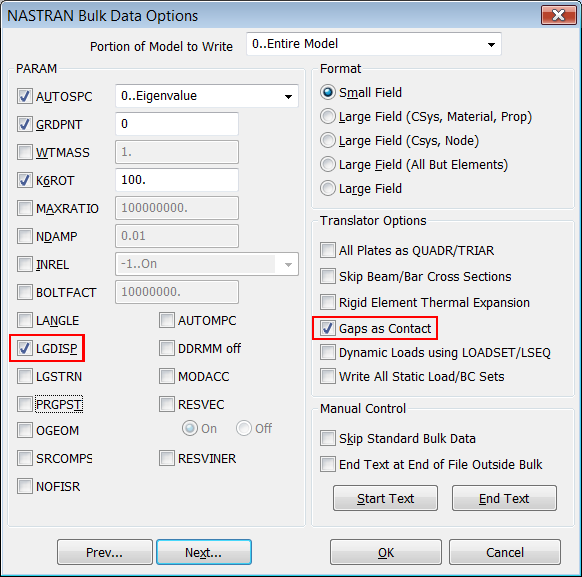
En "NASTRAN Bulk Data Options" activamos la opción "GAPs as Contact" y FEMAP activa automáticamente el parámetro "LGDISP" que le dice al solver que considere la no linealidad geométrica por grandes desplazamientos. |
|
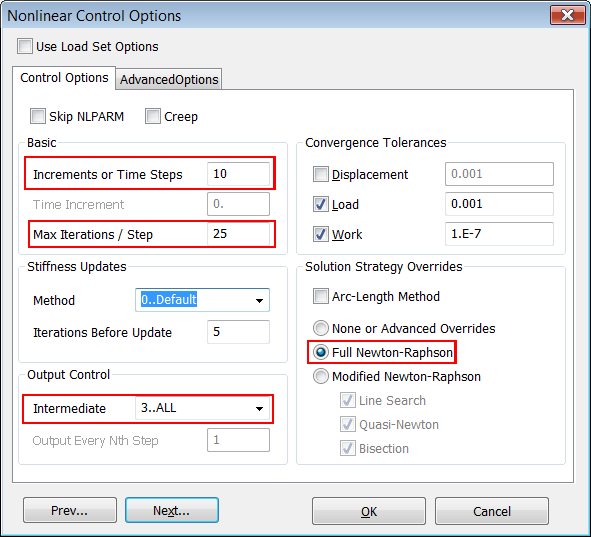
En "Nonlinear Control Options" con "Basic > Number of Increments = 10" le indicamos al solver que como mínimo utilize 10 pasos de tiempo en la solución del problema no lineal, y un máximo de iteraciones por paso de 25. Si la solución no converge se deberá aumentar el nº de incrementos de tiempo, pero en este caso la única no linealidad presente es debida a la geometría y el contacto, por tanto 10 pasos es suficiente. |
| En "Output Control > Intermediate = 3..ALL" le decimos que guarde todos los pasos intermedios de la solución. |
| En "Solution Strategy Overrides = Full Newton-Rapson". |
|
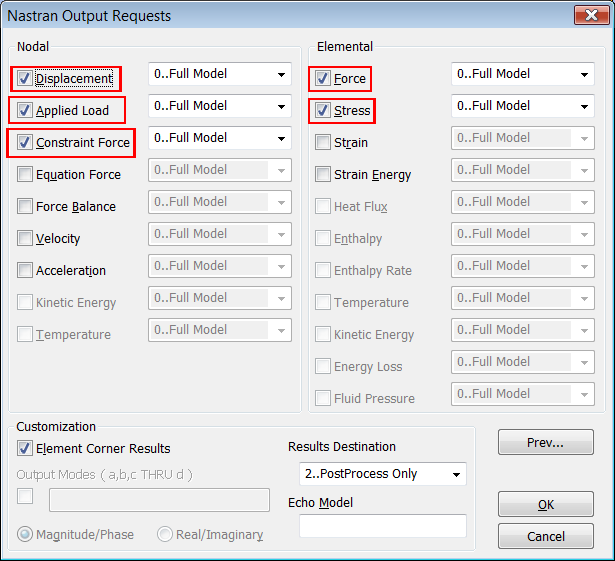
En "Nastran Output Request" activamos el cálculo de esfuerzos, tensiones, desplazamientos, cargas aplicadas y reacciones: |
2. Ejecución del Análisis Estático No Lineal
Para ejecutar el análisis vamos a "Model
> Analysis" y hacemos click en "Analyze":
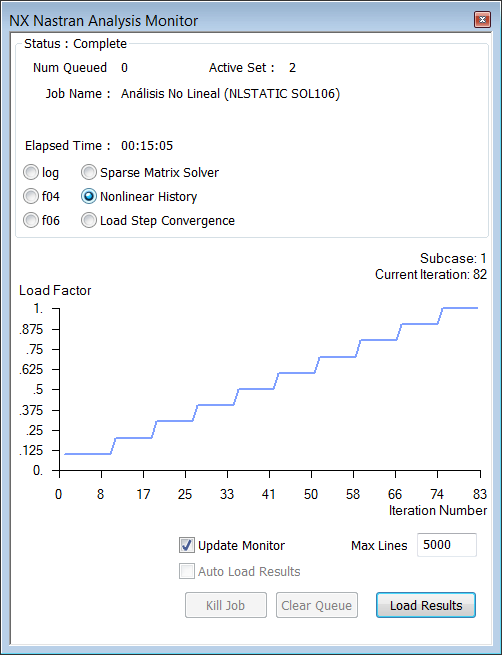
Las siguientes imágenes muestran el "NX NASTRAN Analysis Monitor" donde podemos seguir el progreso de la solución. La imagen de la iquierda muestra el progreso de la solución no lineal, se puede observar que cada paso de tiempo requiere unas 8 iteraciones de convergencia. La imagen de la derecha muestra la gráfica de convergencia de cada paso de análisis, esa imagen en concreto corresponde al último paso del análisis. Tiempo de solución: más de 15 minutos!!.
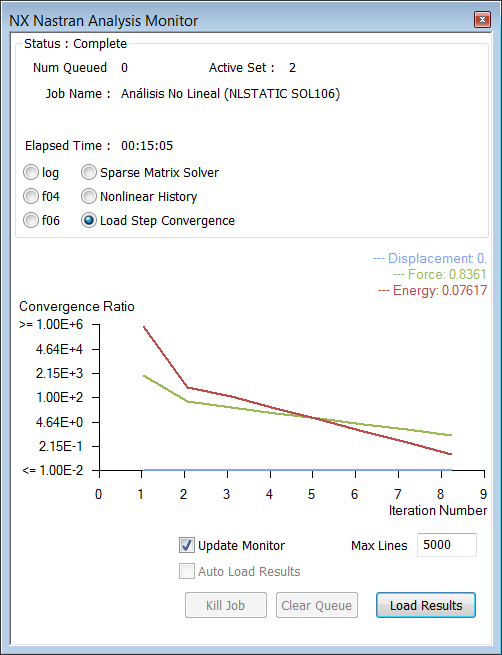
Ejecución del
Análisis Estático No Lineal (NLSTATIC SOL106)
3. Postprocesado de Resultados del Análisis Estático No Lineal
q
3.1. Equilibrio
entre Cargas y Reacciones (N)
Lo primero es comprobar en el fichero de resultados generado por NX
NASTRAN (*.f06) que las reacciones (SPCFORCE RESULTANT) están en equilibrio con
las cargas (OLOAD RESULTANT). En el sistema está en equilibrio,
RFZ=-29475 N.
* * * * * * * * * * * * * * * * * * * *
* * * * * * * * * * * * * * * * * * * *
* * * *
* * * *
* * * *
* * * *
* * N X N a s t r a n * *
* * * *
* * VERSION - 7.0 * *
* * * *
* * SEP 17, 2009 * *
* * * *
* * * *
* *Intel64 Family 6 Model 23 Steppi * *
* * * *
* *Intel(R) Core(TM)2 Quad CPU Q955 * *
* * * *
* * Windows Vista Service Pack 2 * *
* * * *
* * Compiled for X86-64 * *
* * * *
* * * * * * * * * * * * * * * * * * * *
* * * * * * * * * * * * * * * * * * * *
0 OLOAD RESULTANT
SUBCASE/ LOAD
DAREA ID TYPE T1 T2 T3 R1 R2 R3
0 1 FX 6.977163E-13 ---- ---- ---- -3.139723E-11 1.592617E-10
FY ---- 3.981256E-13 ---- 1.791565E-11 ---- 8.701965E-13
FZ ---- ---- 2.947503E+04 -5.297384E+06 -1.608847E+06 ----
MX ---- ---- ---- 0.000000E+00 ---- ----
MY ---- ---- ---- ---- 0.000000E+00 ----
MZ ---- ---- ---- ---- ---- 0.000000E+00
TOTALS 6.977163E-13 3.981256E-13 2.947503E+04 -5.297384E+06 -1.608847E+06 1.601319E-10
0 SPCFORCE RESULTANT
SUBCASE/ LOAD
DAREA ID TYPE T1 T2 T3 R1 R2 R3
0 1 FX -1.065164E-02 ---- ---- ---- 4.793238E-01 -2.894958E+02
FY ---- -1.201129E+00 ---- -5.405081E+01 ---- 2.218288E+02
FZ ---- ---- -2.947502E+03 5.360485E+05 1.608232E+05 ----
MX ---- ---- ---- -6.334357E+03 ---- ----
MY ---- ---- ---- ---- 6.144258E+01 ----
MZ ---- ---- ---- ---- ---- -5.198869E-02
TOTALS -1.065164E-02 -1.201129E+00 -2.947502E+03 5.296601E+05 1.608851E+05 -6.771910E+01
../..0 10 FX -3.528729E-01 ---- ---- ---- 1.587928E+01 -7.401309E+03
FY ---- -4.136375E+01 ---- -1.861369E+03 ---- 5.075858E+03
FZ ---- ---- -2.947495E+04 5.301654E+06 1.608851E+06 ----
MX ---- ---- ---- -4.940076E+03 ---- ----
MY ---- ---- ---- ---- -8.697710E+00 ----
MZ ---- ---- ---- ---- ---- -6.235104E-01
TOTALS -3.528729E-01 -4.136375E+01 -2.947495E+04 5.294852E+06 1.608858E+06 -2.326074E+03
|
q
3.2. Resultados
de Desplazamientos (mm)
La siguiente imagen muestra los valores de desplazamientos
resultantes (a escala exagerada, claro), poco más de 5 mm en una placa de 2 mm de
espesor, este resultado ya está mucho mejor, hemos pasado de un desplazamiento
por encima de los 23 mm a poco más de 5 mm, un factor de 23.1/5.37=4.3
veces!!.
También he incluido la gráfica XY de Carga vs. Desplazamiento que demuestra cómo la relación entre fuerza aplicada y desplazamiento resultante es no lineal. A este fenómeno se le denomina "Stress Stiffening", o endurecimiento por tensión. El término "Stress Stiffening" se refiere al acoplamiento entre la tensión de membrana y el desplazamiento lateral asociado con la flexión. La rigidez de flexión de una viga, arco, placa o Shell aumenta por la tensión de membrana de tracción, y disminuye por la tensión de membrana de compresión. Cuando la tensión de membrana de compresión es elevada puede anular la rigidez de flexión, es decir, la estructura pandea, a este fenómeno se le denomina "Buckling" o también "Stress Softening".
La tensión de membrana se puede considerar despreciable en piezas macizas, pero es muy importante en piezas de pared fina o de espesor reducido como son las estructuras de chapa. Ojo!!, porque mucha gente sigue pensando que el análisis no lineal tiene que ver exclusivamente con la plastificación del material, pero en la vida real los fallos por colapso de la estructura debido a no linealidades geométricas (o sea, pandeo) está a a la orden del día.
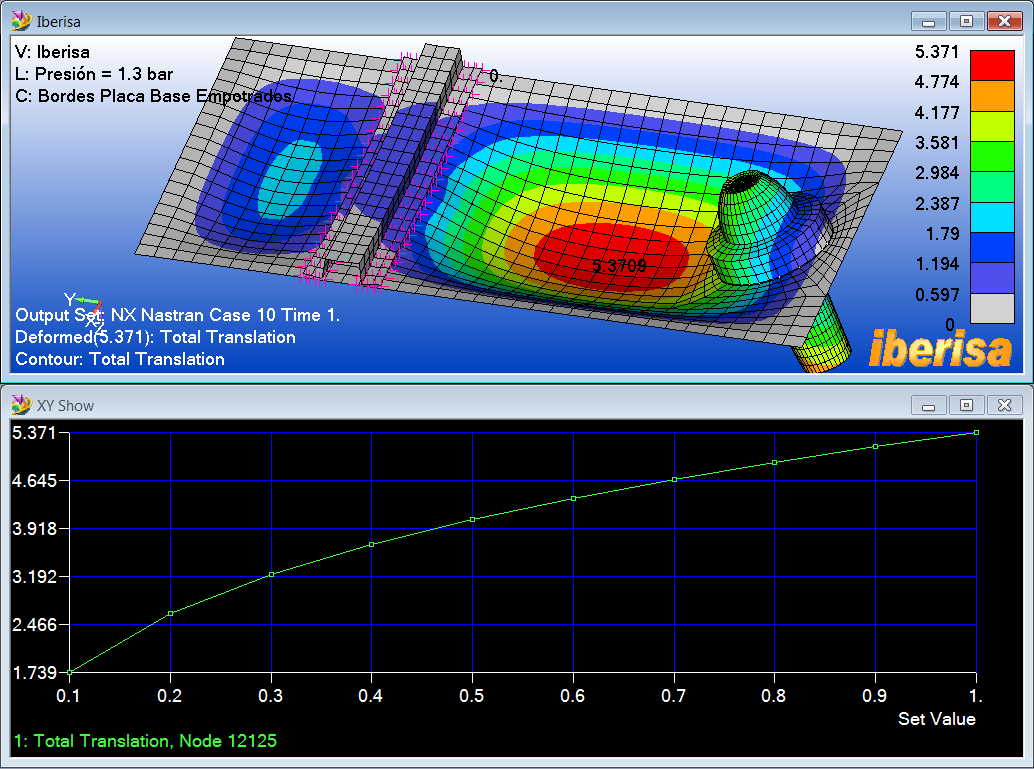
Resultados de desplazamientos (mm) del
Análisis Estático No Lineal (NLSTATIC SOL106)
q
3.3. Resultados
de Tensiones vonMises (MPa)
La siguiente imagen muestra los valores de tensiones vonMises en
los elementos Shell CQUAD4:
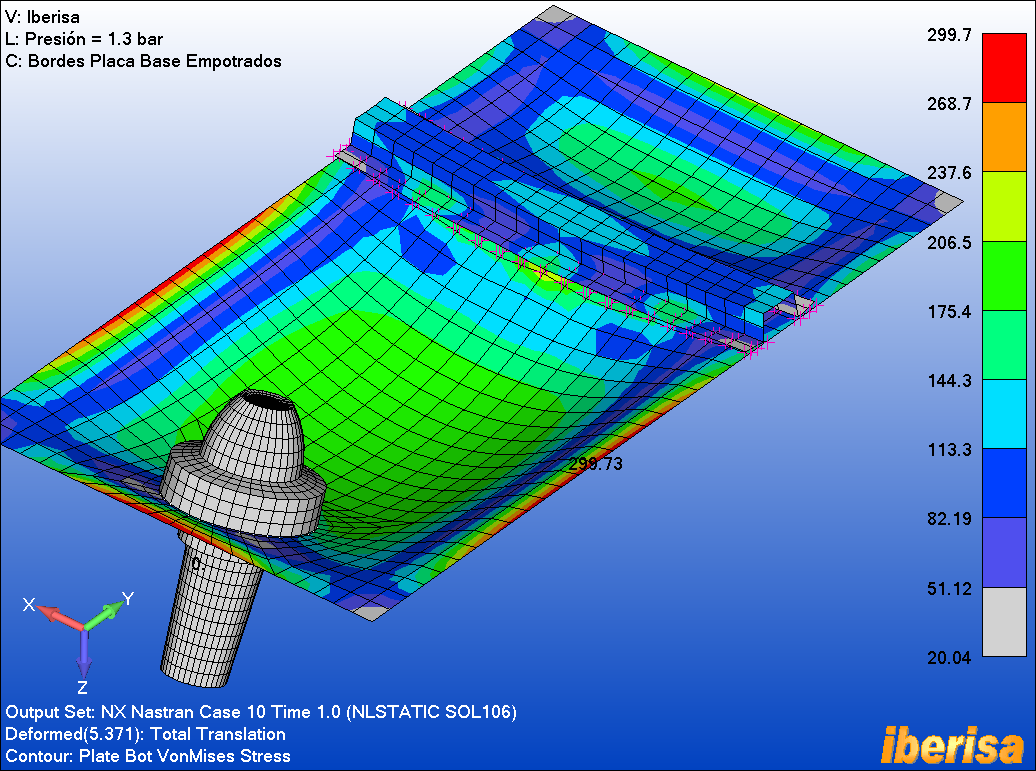
Resultados de tensiones vonMises
(MPa) del
Análisis Estático No Lineal (NLSTATIC SOL106)
Comparando los resultados de máximo desplazamiento entre el análisis estático lineal y no lineal se aprecia que para el mismo nivel de carga el valor del análisis no lineal es menor que el análisis lineal, es decir, la estructura es más rígida. Este comportamiento no lineal se conoce con el nombre de "Stress Stiffening" o rigidización por tensión: consiste en un acoplamiento de la tensión de membrana y el desplazamiento lateral asociado con la flexión. Este efecto de rigidez de membrana únicamente se puede capturar mediante un análisis no lineal por la geometría. Así, a mayor carga que produzca estados de tensión a tracción en la estructura, mayor rigidez. El efecto contrario se conoce como "Stress Softening", o Pandeo, aparece cuando la estructura trabaja a compresión y puede causar el colapso de la estructura.
Aquí concluye el Tutorial de Análisis Estático Lineal y No Lineal con Uniones Soldadas Pto-a-Pto y Contactos nodo-a-nodo, espero que os haya resultado interesante y útil a la vez.
Saludos,
Blas.
SÍGUENOS
EN: 
