FEMAP V10.1 & NX Nastran 6.1 Tutorial
Pandeo Clásico de Euler en una Viga Bi-apoyada
(Octubre, 2009)
El objetivo de este Tutorial es aprender a resolver un problema clásico de pandeo lineal de una viga bi-apoyada, también conocido como "Pandeo de Euler Clásico".
1. Descripción del Problema
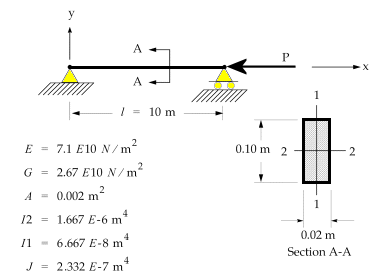
Una carga de compresión de valor FX=-1000 N se aplica en
el apoyo de rodillos de la viga plana bi-apoyada de sección rectangular de
dimensiones de la sección A = 0.10 m x 0.02m y longitud L=10m para generar
cargas internas en la estructura. Se pide calcular los cinco primeros modos de
pandeo de la viga utilizando el Método de Lanczos de extracción de valores
popios. En este problema la viga se puede mallar con elementos CBAR o CBEAM, en
esta ocasión utilizaremos el elemento CBAR. El pandeo ocurrirá en el
plano X-Z ya que el Momento de Inercia Iyy es mucho menor que el momento de
inercia Izz.
2. Definición del Modelo de Elementos Finitos
q
2.1.
Definición
de la Geometría
En primer lugar desde "Geometry >
Curve - Line > Coordinates" definimos la línea de centro de la viga
entre las coordenadas (0,0,0) y (10,0,0). Trabajaremos en el sistema de unidades
internacional (SI), con las cargas en Newton (N), la longitud en metros (m) y la
tensión en Pascal (Pa, N/m2).
q
2.2.
Definición
de la Densidad de Malla
Desde "Mesh > Mesh Control >
Size Along Curve .." seleccionamos la línea creada anteriormente y le
asignamos una densidad de malla (nº de elementos) de 10. Para ver la densidad
de malla asignada a la curva pulsa en "F6 > Labels, Entities and
Colors > Curve - Mesh Size > Draw Entity ON > 3...Symbols and Count
> OK".
q
2.3.
Asignación de
Atributos a la Curva
Desde "Mesh > Mesh Control >
Attributes Along Curve .." seleccionamos la línea creada anteriormente
y le asignaremos el material y las propiedades del tipo de elemento. Así, en
vez de utilizar el método "de manual" de definir primero materiales,
seguidamente popiedades de elementos y por último asignar propiedades a la
geometría, en este caso lo vamos a hacer todo al "vuelo". Pues bien,
empezamos:
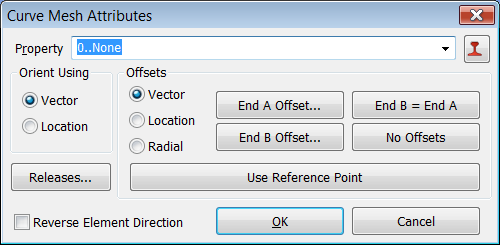
En "Curve Mesh Attributes"
haz click sobre el botón 
para crear una nueva propiedad y asignarla a la curva-eje longitudinal de la
viga:
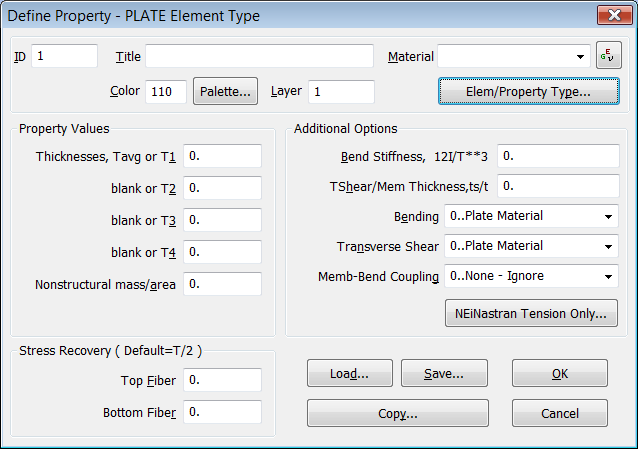
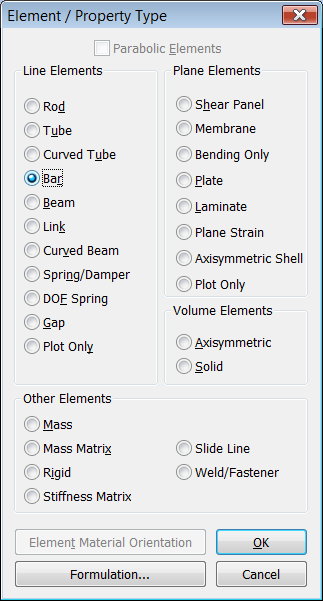
En la siguiente ventana "Define Property - PLATE Element Type" pulsamos sobre el botón "Element/Property Type..." y seleccionamos el tipo de elemento "BAR" que en NX Nastran se corresponde con el elemento CBAR:
Nos aparece una ventana con todos los campos en blanco para introducir las propiedades del elemento BAR. En primer lugar recomiendo meter un título, por ejemplo "Viga Rectangular (0.1mx0.02m)", y en vez de meter los valores numéricos "a mano" dejaremos que los calcule FEMAP usando una sección de la librería de perfiles, para lo cual pulsamos en el botón "Shape":
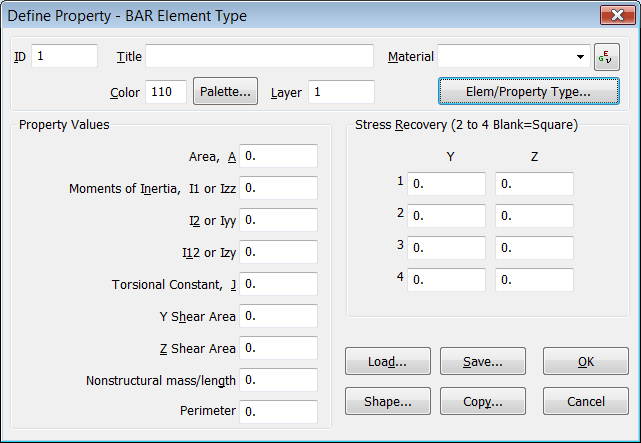
Desplegamos el botón "Shape" y seleccionamos el tipo de sección "Rectangular Bar" y metemos las dimensiones de la sección "Height = 0.1" y "Width = 0.02". Otra cosa que me gusta hacer es definir el eje-Y en vertical como eje principal de inercia de la sección pulsando sobre "Up" en el campo "Orientation Direction (Y)". Pulsamos OK:
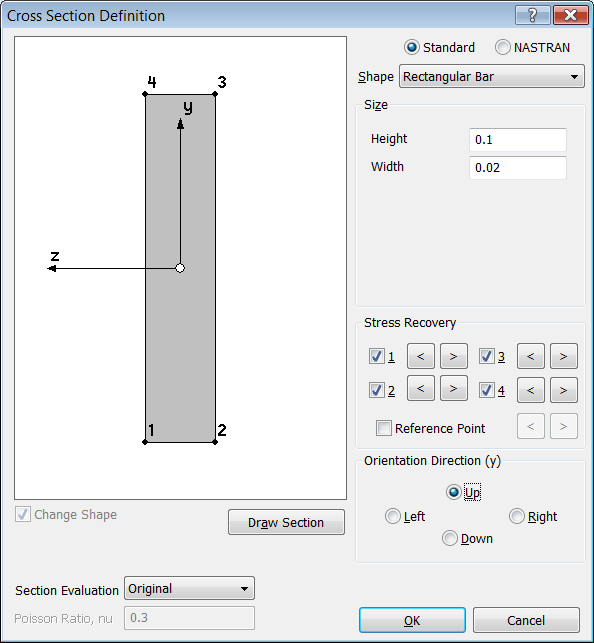
Y en la siguiente imagen vemos que FEMAP rellena todos los
campos con las propiedades de inercia de la sección introducida anteriormente.
Vemos que se corresponden perfectamente con los valores del enunciado del
problema. Si damos al botón OK vemos que FEMAP nos obliga a asignar un material
junto a las propiedades del elemento, es un buen método para que no nos
olvidemos de asignar un material al elemento, así que pulsamos sobre el botón 
para definir un nuevo material:
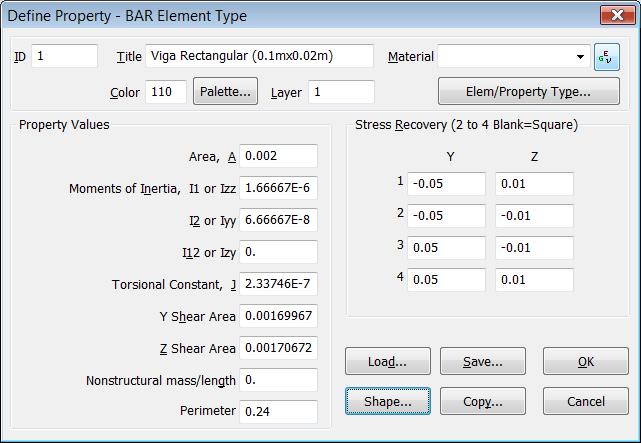
Metemos las propiedades del material, que por sus valores veo que se trata de Aluminio. A mí me gusta poner en el título del material el nombre y el sistema de unidades en el que están definidas las propiedades del material, así si alguien abre el modelo tendrá claro de qué material se trata y sus unidades simplemente por el título:
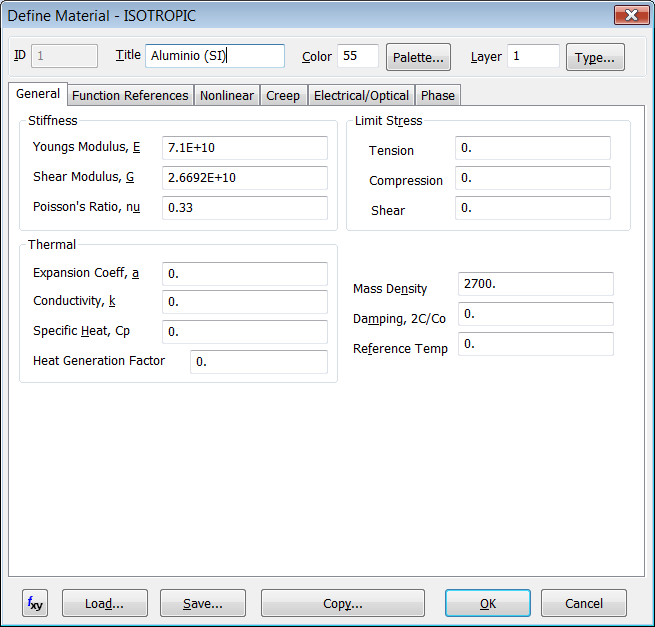
Seguidamente pulsamos OK en la ventana "Define Material - ISOTROPIC", de nuevo OK en la ventana "Define Property - BAR Element Type", y regresamos a la ventana original de "Curve Mesh Attributes" en la cual en el campo "Property" seleccionamos la propiedad anteriormente definida. En esta ventana tenemos numerosas opciones que nos permitirán definir la orientación de la viga mediante un vector o la posición de un punto, el "OFFSET End-A/End-B" de la misma o los "END RELEASE CODES End-A/End-B" que es un método para liberar grados de libertad de los nodos extremos de una viga. Seleccionamos la opción "Orient Using -- Vector" y pulsamos OK:
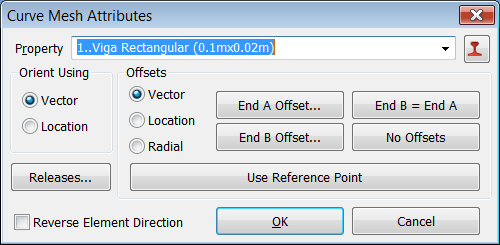
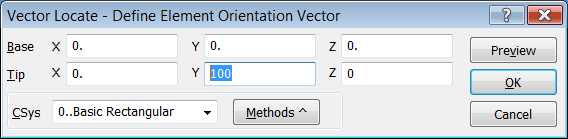
Nos aparece una ventana solicitando la definición de un vector, por ejemplo utilizamos "Base (0,0,0)" y "Tip (0,1,0)", de esta forma estamos orientando el eje principal de inercia de la sección (eje-Y local) de la viga que sea paralelo al eje-Y del sistema de coordenadas global cartesiano "0..Basic Rectangular"
q
2.4.
Mallado de la Curva
con Elementos CBAR
Desde "Mesh > Geometry > Curve "
seleccionamos la curva y la mallamos haciendo click en OK en la siguiente
ventana:
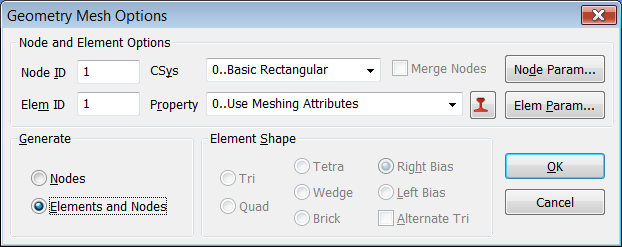
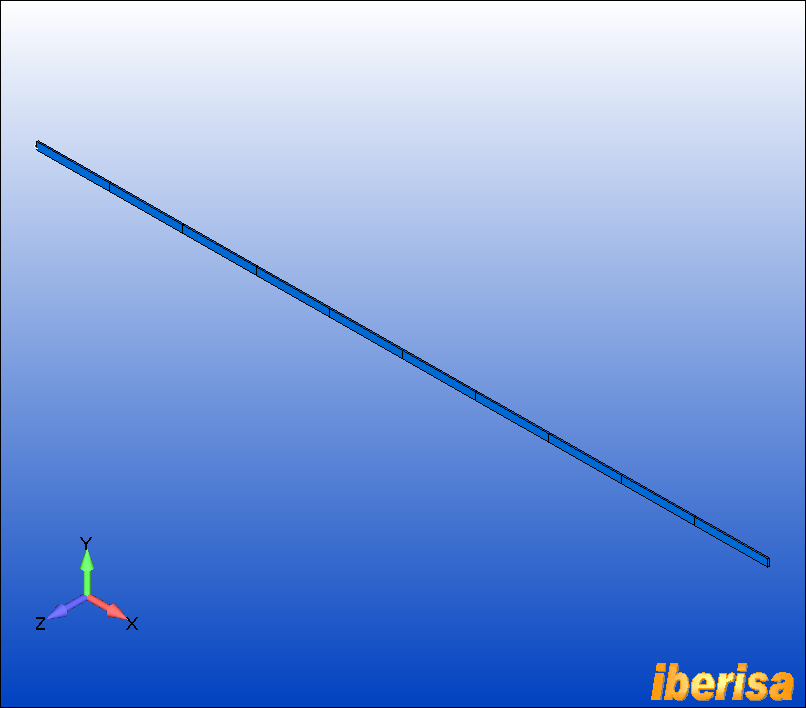
Para ver la viga representada en 3D con su sección transversal ir a "F6 > Labels, Entities and Colors > Element - Orientation/Shape > 3...Show Cross Section > OK" y verás algo similar a la siguiente imagen:
q
2.5.
Definición de las
Condiciones de Contorno
Desde "Model > Constraint >
Nodal" creamos un nuevo set de restricción, por ejemplo
"Constraint#1", seleccionamos el nodo#1 situado en el extremo
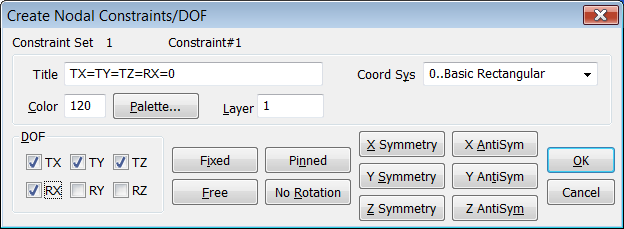
izquierdo de la viga y definimos las restricciones TX=TY=TZ=RX=0 que corresponde
a un apoyo articulado y además limitamos la rotación alrededor del eje de la
viga ya que de lo contrario el solver nos daría error de matriz singular al
estar libre el grado de libertad de torsión:
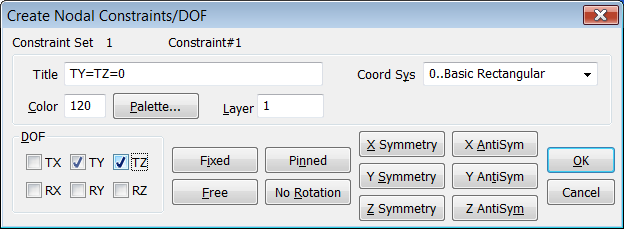
Repetimos de nuevo desde "Model > Constraint > Nodal" , seleccionamos el nodo#11 situado en el extremo derecho de la viga y definimos el apoyo de rodillos haciendo TY=TZ=0 dejando libre el desplazamiento en la direción del eje-X:
q
2.6.
Definición de
Cargas
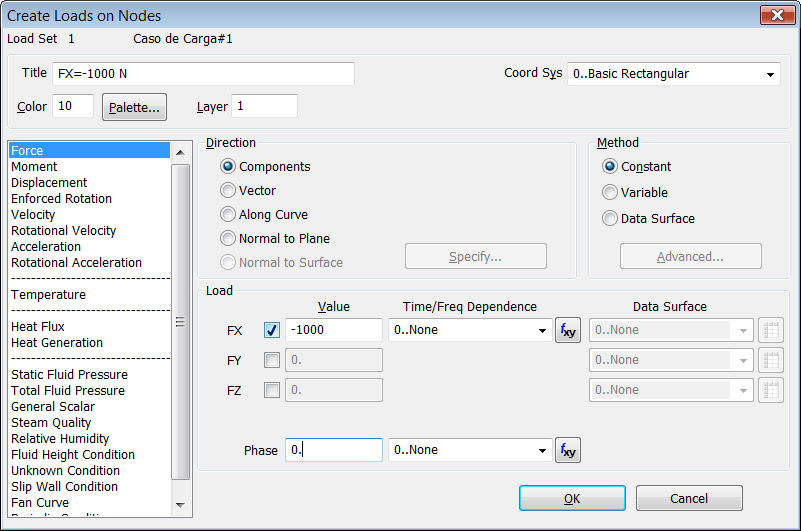
Desde "Model > Loads > Nodal"
creamos un nuevo set de caso de carga, por ejemplo "Caso de Carga#1",
seleccionamos el nodo#11 situado en el extremos derecho de la viga (en el apoyo
de rodillos) y aplicamos la carga FX=-1000N:
3. Definición del Análisis de Pandeo Lineal
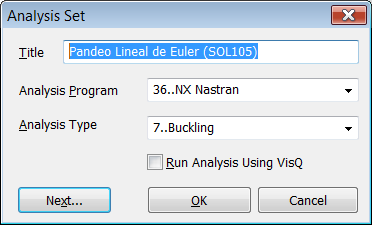
Desde "Model > Analysis > Analysis Set Manager
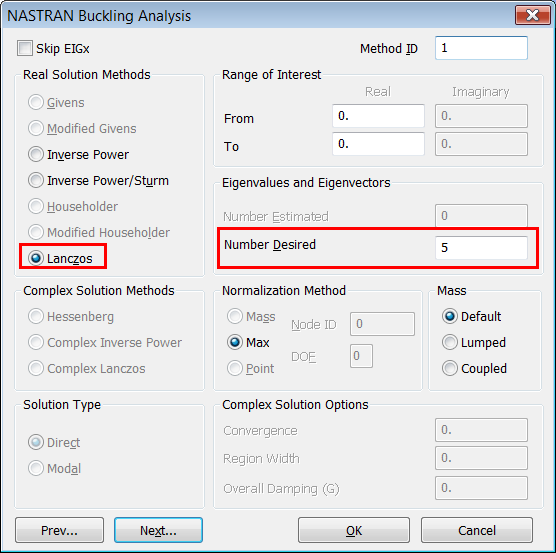
> New" creamos el análisis de Pandeo Lineal "7..Buckling"
con el solver NX Nastran y solicitamos el cálculo de los cinco primeros modos
de pandeo de la viga utilizando el Método de Extracción de Valores Propios de
Lanczos:
4. Postprocesado de Resultados
El siguiente listado muestra los resultados del fichero *.F06
del salida de resultados gnerado por el solver NX Nastran con los cinco primeros
modos de pandeo de la viga. El valor del primer modo de pandeo ("eigenvalue")
es λ1 = 0.4672 para un valor de la carga
aplicada FX = –1000 N. Por tanto, el valor del primero modo de pandeo de la
viga será igual a:
P1 =( λ1) (Pa) = (0.4672) (-1000) = -467.2 N
E I G E N V A L U E A N A L Y S I S S U M M A R Y (READ MODULE)
BLOCK SIZE USED ...................... 7
NUMBER OF DECOMPOSITIONS ............. 3
NUMBER OF ROOTS FOUND ................ 5
NUMBER OF SOLVES REQUIRED ............ 26
R E A L E I G E N V A L U E S
MODE EXTRACTION EIGENVALUE RADIANS CYCLES GENERALIZED GENERALIZED
NO. ORDER MASS STIFFNESS
1 1 4.671651E-01 6.834948E-01 1.087816E-01 4.934667E+02 2.305304E+02
2 2 1.868976E+00 1.367105E+00 2.175815E-01 2.181378E+03 4.076942E+03
3 3 4.208506E+00 2.051464E+00 3.265007E-01 4.431846E+03 1.865145E+04
4 4 7.497434E+00 2.738144E+00 4.357892E-01 4.973294E+03 3.728694E+04
5 5 1.168143E+01 3.417079E+00 5.438451E-01 4.934653E+02 5.761913E+03 |
Nótese que los primeros cuatro modos de pandeo de la viga se desarrollan en el plano X-Z, y el primer modo de pandeo en el plano X-Y es el quinto modo de pandeo. Por tanto, la carga más baja de pandeo en el plano X-Y será igual a:
P5 =(λ1) (Pa) = (1.1681) (-1000) = -11681 N
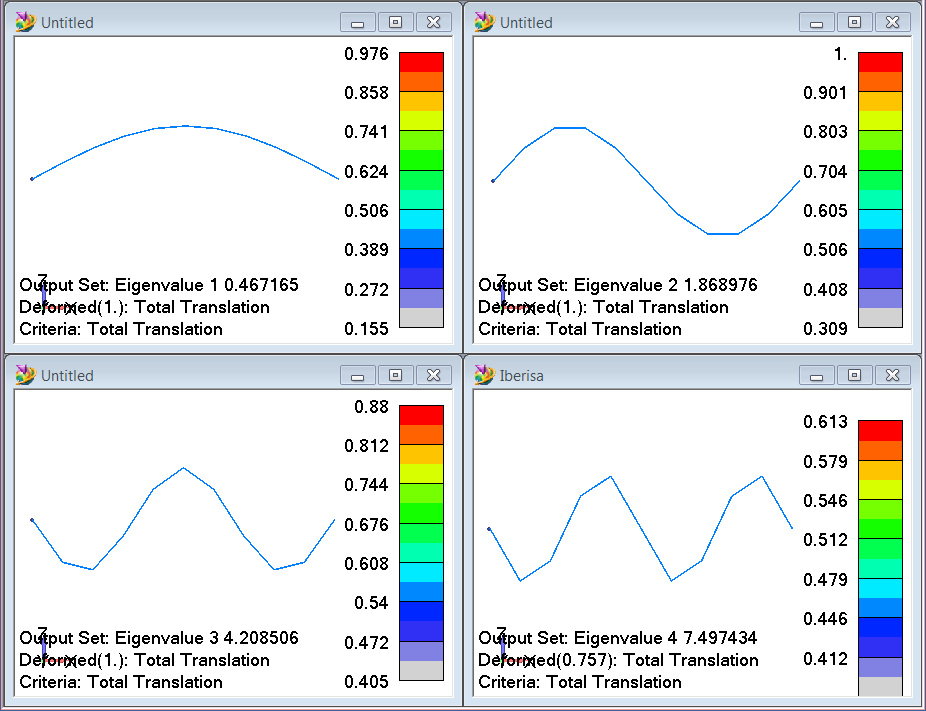
Postprocesado de Resultados en FEMAP
4. Comparación con la Solución Teórica
El Pandeo de Euler se calcula como sigue (S.P. Timoshenko and
J.M. Gere, Theory of Elastic Stability, Engineering Societies Monograph
Series, Second Ed., 1961):
|
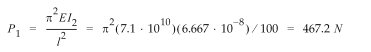
Modo de Pandeo |
NX Nastran (N) |
Teoría (N) |
% Diferencia |
|
|---|---|---|---|---|
|
1 (Plano X-Z) |
467.2 |
467.2 |
0 |
|
|
5 (Plano X-Y) |
11681.5 |
11681.4 |
0.001 |
|
Según nos aproximamos a los modos superiores, la forma del modo es cada vez menos suave. Este efecto ocurre porque a igualdad de densidad de malla, los modos superiores tienen menos elementos por cada onda senoidal de pandeo que los modos inferiores. Si estás interesado en calcular los modos superiores, deberás incrementar la densidad de malla del modelo para seguir la regla general de tener un mínimo de seis elementos por cada media onda senoidal. De todas formas, los modos de pandeo superiores son de nulo interés en las aplicaciones reales.
Espero que el tutorial os haya resultado útil e interesante!!.
Saludos,
Blas.
SÍGUENOS
EN: 
