FEMAP V11.0.1 & NX Nastran 8.5.1 Tutorial
Heat Transfer from a Chip to PCB with GLUE
Surface-to-Surface Thermal Coupling
(Mayo, 2013)

 

1. Problem Description
The main target of this tutorial is to learn how to define materials in FEMAP with Orthotropic properties and also the thermal coupling between PCB and Chip using the powerful GLUE Surface-to-Surface Contact capability of the Simcenter NASTRAN finite element solver.

A Printed Circuit Board (PCB) will be subject to a heat generation load applied to the chip. The temperature of the back side of the plate is 45º C and the ambient temperature of the system is 30º C. The PCB is made of a composite orthotropic material, and the chip is made of an isotropic material with a higher thermal conductivity. A temperature will be calculated at each node in the model using the Steady-State Heat Transfer capability of NX Nastran (SOL153). Free Convection will be used to allow heat to transfer between both the top and side faces of the CHIP and the top of the PCB and the surroundings.

The loads & boundary conditions are the following:

Heat load Q= 5 Watt applied to the top surface of the chip.

Temperature constraint of 25°C applied to the edge of the PCB opposite to the edge closest to the chip.

Convection coefficient applied on the top and side faces of the chip averaged to a single value of 24 W/m2ºC.

Convection constraint to the top face of the PCB with a lower heat transfer coefficient of 19 W/m2ºC, being 25ºC the ambient temperature of the fluid around the PCB.

Thermal coupling between the CHIP & PCB. Assume the chip is connected to the PCB using a Ball Grid Array (BGA) solder connection with a total area that is half of that of the chip. Assume as well a Pb-Sn weld of thermal conductivity Ksolder= 80 W/mºC and a gap of 1 mm. We can then calculate the total conductance as follows: 

Heat Transfer Coefficient = ksolder * Asolder / (Lgap * Achip) = 80*0.5/ 0.001*1 = 40e3 W/m2ºC


FEMAP model of the Chip & PCB assembly

 

2. Import the CAD model in FEMAP
Import the CAD model in Parasolid using "FILE > IMPORT > GEOMETRY", to avoid mistakes make sure to use a "Geometry Scale Factor = 1000", this way the geometry will be in "mm" instead inches or other system of units.


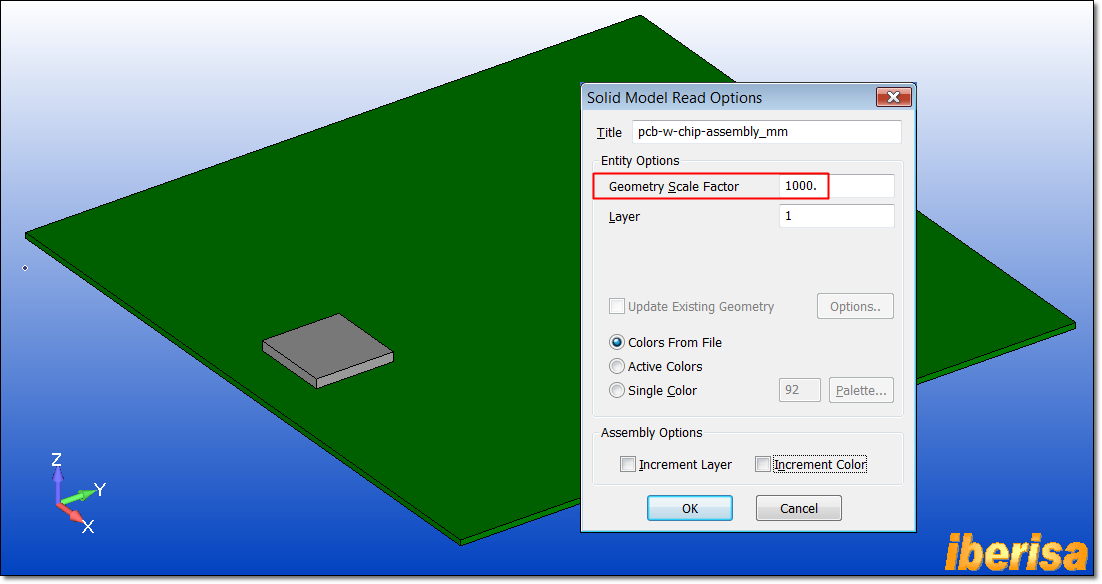
CAD model assembly of Chip and PCB

 

3. Define the Orthotropic Material Properties for the PCB
Let´s start by creating an orthotropic material for the PCB using "MODEL > MATERIAL > TYPE > ORTHOTROPIC (2D)" with the MAT5 entry card of NX NASTRAN. The material density is 2700 kg/m3, specific heat is 396 J/kg-K, and the orthotropic thermal conductivity is 0.009 W/mm-C, 0.041 W/mm-C, and 0.00055 W/mm-C in the X, Y and Z directions (please note the consistent system of units used based in N, mm & Tons!!)

Propiedad Valor
Mass density, DENS 2700e-12 Ton/mm3
Specific Heat, Cp 396e+3 J/TonºC
Thermal Conductivity (KXX) 0.009 W/mmºC
Thermal Conductivity (KXX) 0.041 W/mmºC
Thermal Conductivity (KXX) 0.00055 W/mmºC

 


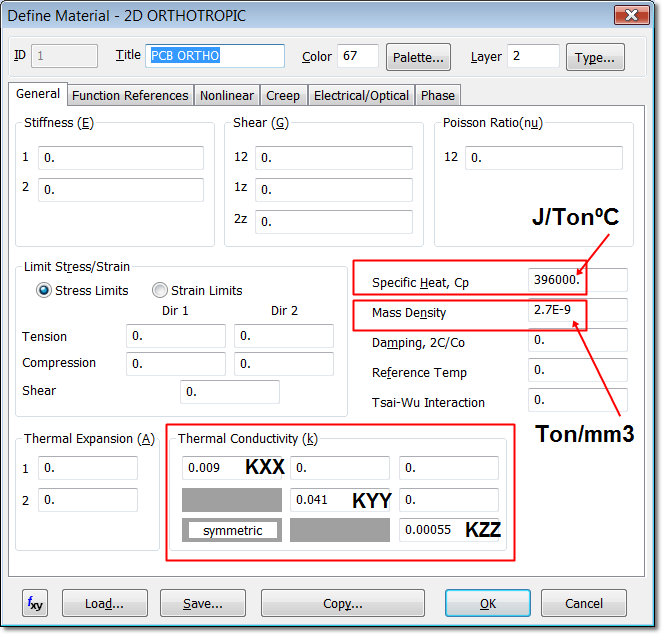
Orthotropic Material Properties for the PCB

 

According the "NX NASTRAN USER's Guide" manual:

Material Properties for Heat Transfer

Material properties for heat transfer analysis are defined using MAT4, MAT5, MATT4, MATT5, RADM and RADMT entries.

* The MAT4, MAT5, and RADM entries provide temperature independent (constant valued) material properties.

* The MATT4, MATT5, and RADMT entries supply information about temperature-dependent properties through reference to material tables (TABLEMi (i = 1, 2, 3, 4)).

With heat transfer material properties:

* Although the surface characteristics for free convection (heat transfer coefficient) and radiation (emissivity and absorptivity) are not normally considered to be material properties, they are included in the bulk entries described here.

* Temperature dependence of the quantity of interest is ultimately defined on a TABLEMi entry. For example, the table is connected to the MAT4 through the MATT4 entry. Most material properties are directed toward a structural element and are referenced by the property entry for the element of interest.

 

Understanding MAT4 and MATT4

The MAT4 bulk entry lets you define thermal properties for temperature-independent isotropic materials .The format of the MAT4 bulk entry is:

1

2

3

4

5

6

7

8

9

10

MAT4

MID

K

CP

ρ

H

μ

HGEN

REFENTH

  
 

TCH

TDELTA

QLAT

            

where:

Symbol

Property

Consistent Units

K(T)

Thermal Conductivity*

W/m °C

CP(T)

Specific Heat*

J/kg °C

ρ

Density*

kg/m3

H(T)

Free Convection Heat Transfer Coefficient

W/m2 °C

μ (T)

Dynamic Viscosity*

N sec/m2

HGEN(T)

Volumetric Internal Heat Generation

W/m3

REFENTH

Reference Enthalpy

J/kg

TCH

Lower Temperature Limit for Phase Change

°C

TDELTA

Temperature Range for Phase Change

°C

QLAT

Latent Heat

J/kg

* Thermal conductivity, specific heat, density, and dynamic viscosity cannot be time dependent. Thermal heat flux loads can reference explicit functions of time. Thermal boundary conditions for convection and radiation utilize control node techniques for specifying time dependent behavior.

The MATT4 entry lets you define temperature-dependent material properties in conjunction with MAT4. NX Nastran always multiplies the basic quantities you specify on the MAT4 entry by the corresponding tabular function (TABLEMi bulk entries) that you reference with the MATT4 entry.

 

Understanding MAT5 and MATT5

The MAT5 bulk entry lets you define thermal properties for temperature-independent anisotropic materials. The MATT5 entry lets you define temperature-dependent material properties in conjunction with MAT5. NX Nastran always multiplies the basic quantities you specify on the MAT5 entry by the corresponding tabular function (TABLEMi bulk entries) that you reference with the MATT5 entry.

 

MAT5

Thermal Material Property Definition

Defines the thermal material properties for anisotropic materials.

Format:

1

2

3

4

5

6

7

8

9

10

MAT5

MID

KXX

KXY

KXZ

KYY

KYZ

KZZ

CP

  
 

RHO

HGEN

              

Example:

MAT5

24

.092

    

.083

  

0.20

0.2

  
 

2.00

                

Fields:

Field

Contents

MID

Material identification number. (Integer > 0)

Kij

Thermal conductivity. (Real)

CP

Heat capacity per unit mass. (Real ≥ 0.0 or blank)

RHO

Density. (Real > 0.0; Default = 1.0)

HGEN

Heat generation capability used with QVOL entries. (Real ≥ 0.0; Default = 1.0)

Remarks:

1. The thermal conductivity matrix has the following form:

2. The material identification number may be the same as a MAT1, MAT2, or MAT3 entry but must be unique with respect to other MAT4 or MAT5 entries.

3. MAT5 materials may be made temperature-dependent by use of the MATT5 entry.

4. When used for axisymmetric analysis (CTRIAX6), material properties are represented where:

KXX = radial conductivity component

KYY = axial conductivity component

Remarks related to SOL 601:

1. MAT5 defines the thermal properties for material with orthotropic thermal conductivity. KXY, KXZ and KYZ are ignored.

 

4. Define the Isotropic Material Properties for the CHIP
To model the chip we will use a 3D solid hexahedral CHEXA 8-nodes mesh and isotropic material with the following values: density 2700e-12 Ton/mm3, Thermal Conductivity KXX = 383e-3 W/mmºC, and Specific Heat Cp = 380e3 J/TonºC with the MAT4 entry of NX NASTRAN.

Propiedad Valor
Mass density, DENS 2700e-12 Ton/mm3
Specific Heat, Cp 380e+3 J/TonºC
Thermal Conductivity, KXX 383e-3 W/mmºC

 


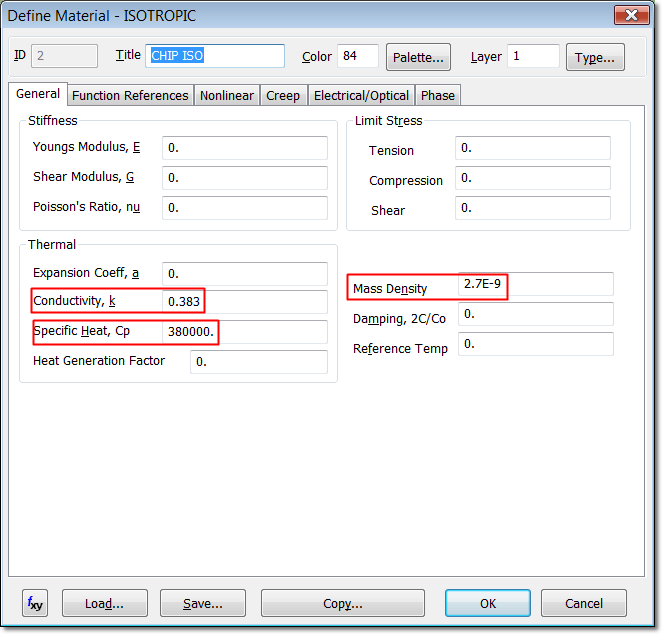
Isotropic Material Properties for the PCB

 

5. Define the Plate Properties for the PCB
Using "MODEL > PROPERTIES > ELEMENT/PROPERTY TYPE => PLATE" define a plate element property and apply the orthotropic material you just created. The thickness of the printed circuit board (PCB) is 1.8 mm.


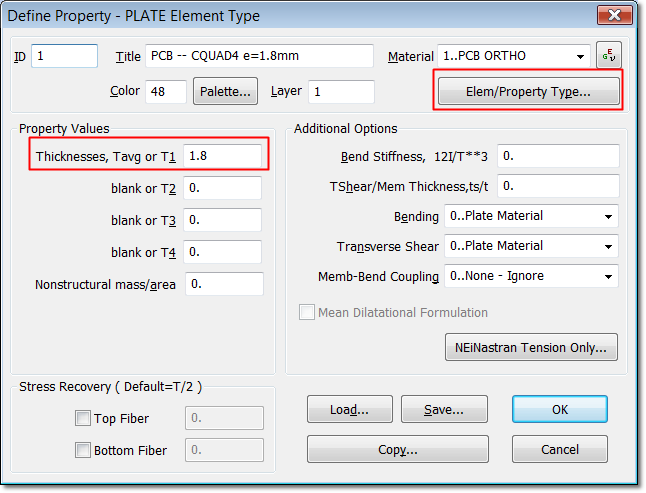
Plate element property for the PCB

 

6. Define the Solid Properties for the CHIP
Using "MODEL > PROPERTIES > ELEMENT/PROPERTY TYPE => SOLID" define a 3-D Solid element property and apply the isotropic material you just created.


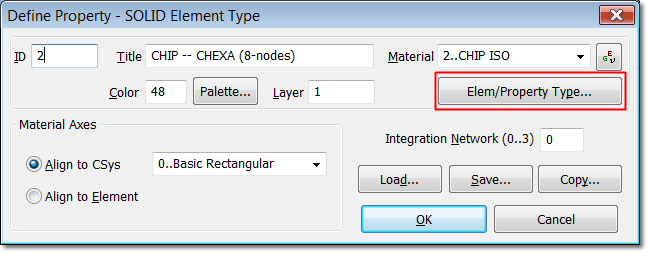
Solid element property for the CHIP

 

7. Create the Mid-Surface for the PCB
First at all when working with midsurfaces I strongly suggest to create a new LAYER where to include the new midsurfaces created. Simply click on "LAYER > NEW" and create the layer named "MIDSURFACE PCB", when you create a new layer it is automatically activated, then any output geometry will be to there.

To generate the midsurface of the PCB use the command "GEOMETRY > MIDSURFACE > OFFSET TANGENT SURFACES..", click on the top face of the PCB and answer with OK all the questions. Click NO when asked to delete the original solid. The result will be a new surface, if you HIDE the LAYER "1.. Default Layer" the new midsurface will be isolated in the screen.


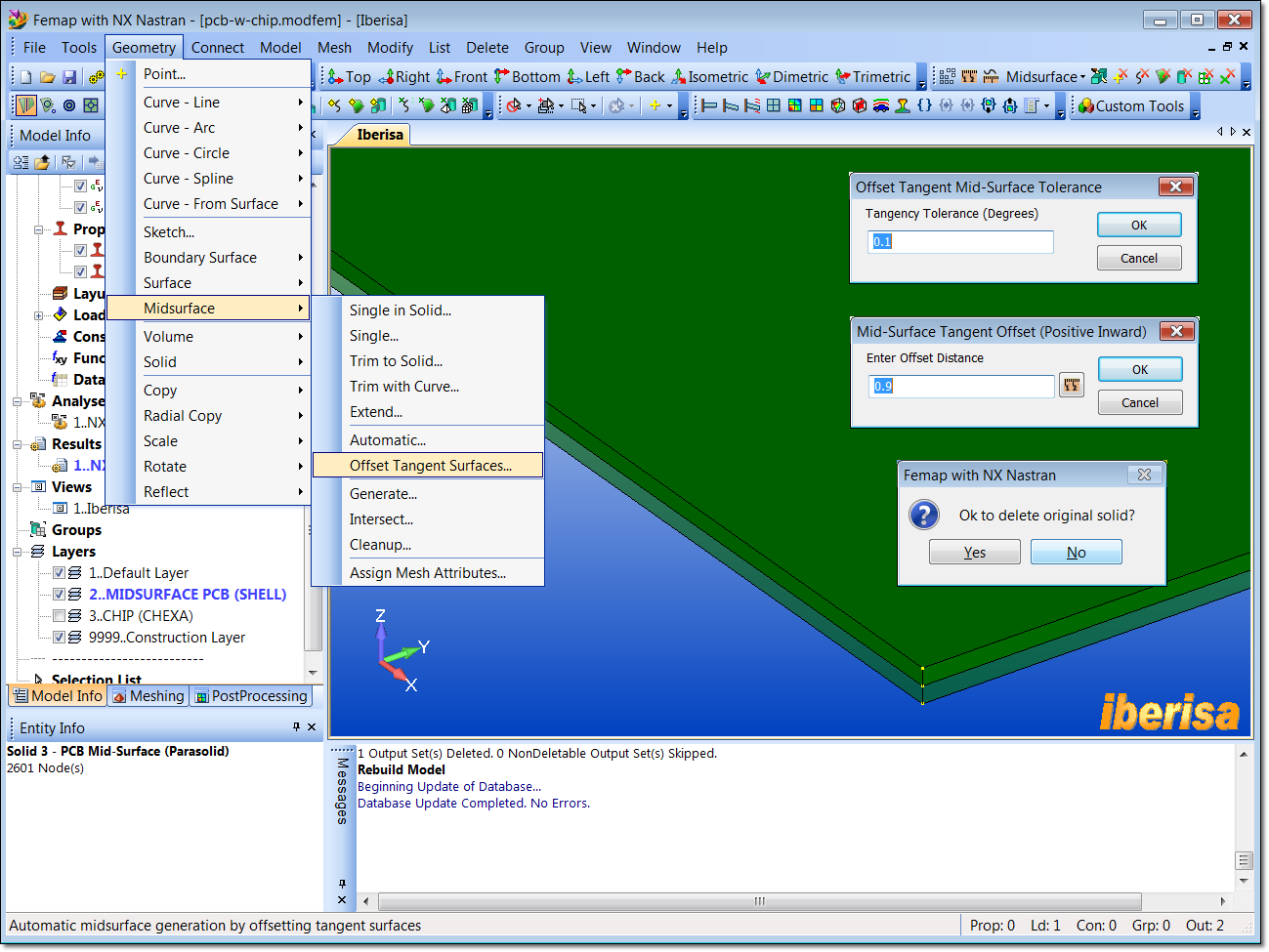
Midsurface creation for the PCB

 

8. Create a 2-D Shell Mesh of the MidSurface for the PCB
First at all let's prescribe meshing attributes to the new midsurface created using "Mesh > Mesh Control > Attributes On Surface" and click on the midsurface of PCB. In the Surface Mesh Attribute > Property form browse and select the plate property for the PCB:


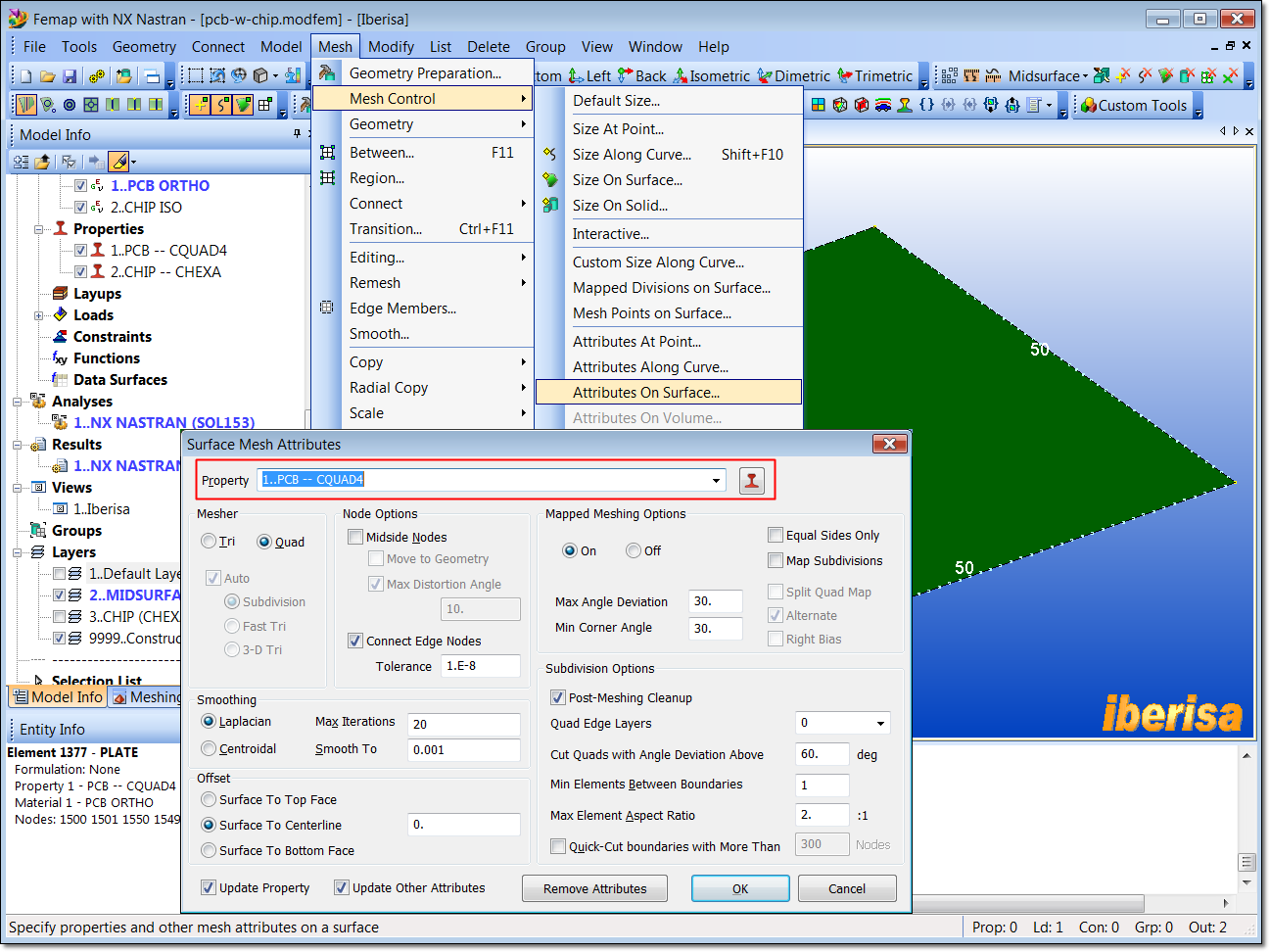
Prescribing Mesh Attributes to MidSurface of PCB to mesh with 2-D Plate CQUAD4 elements

 

The next step will be to prescribe the mesh size on the PCB using "Mesh > Mesh Control > Size On Surface" and click on the midsurface of PCB. In the "Automatic Mesh Sizing > Element Size" field enter a value of 200/50 (please note Esize = Lengthcurve/Nelements) this will prescribe 50 divisions along the curve edges of the PCB midsurface of length 200 mm.


Prescribing Mesh Size to MidSurface of PCB to mesh with 2-D Plate CQUAD4 elements

 

To visualize the mesh size on geometry make sure that curves are visible in the screen and also click "F6" and make sure to select all the options of the following picture:


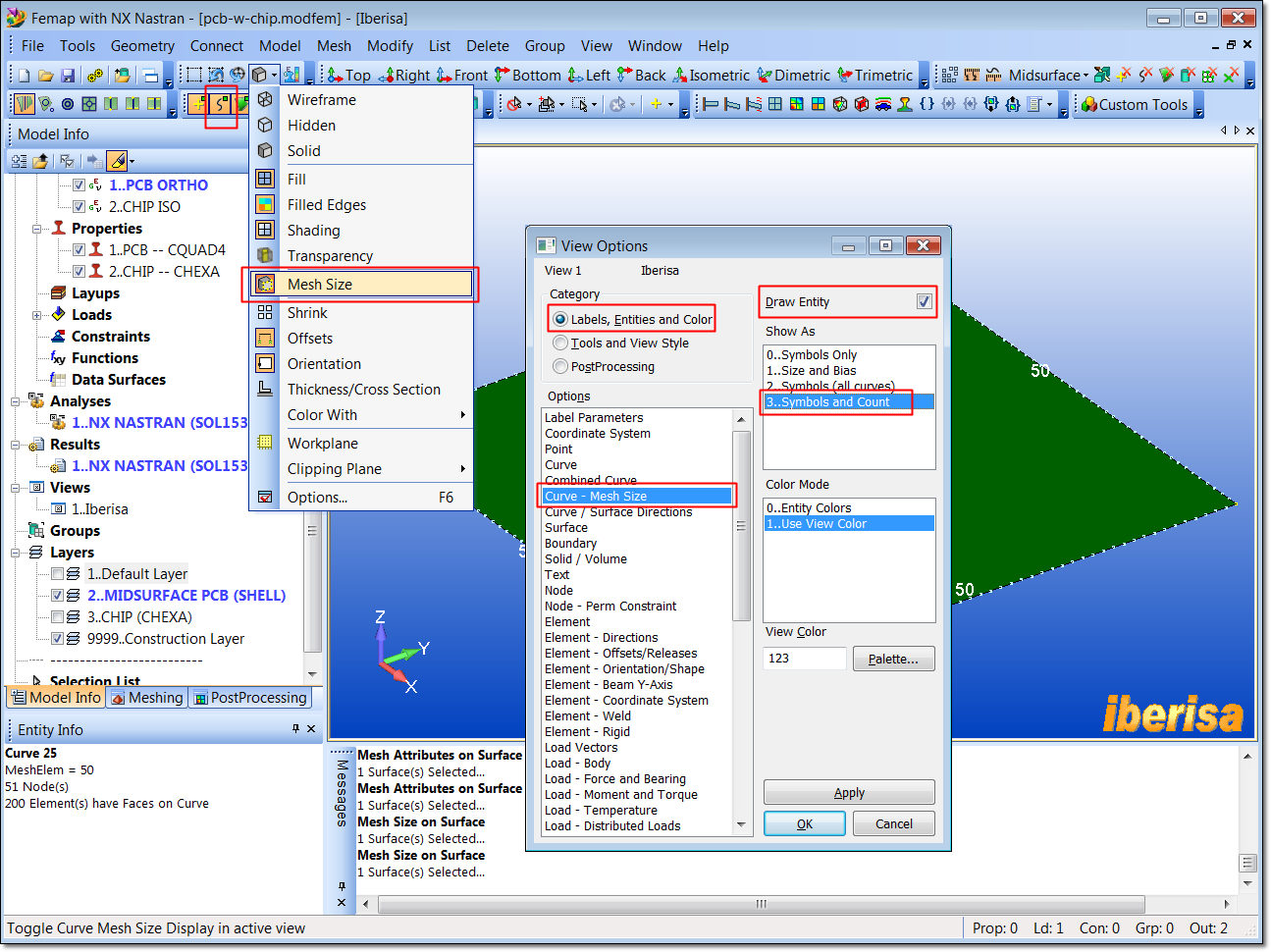
Visualizing Mesh Size on Curves

 

And finally mesh the PCB midsurface with 2-D plate CQUAD4 elements using "Mesh > Geometry > Surface" and click on the midsurface of PCB. In the "Automesh Surfaces > Property" field make sure that appear the option "0..Use Meshing Attributes", this means that you have done the job correctly prescribing meshing properties to the geometry, if not please repeat the steps above.


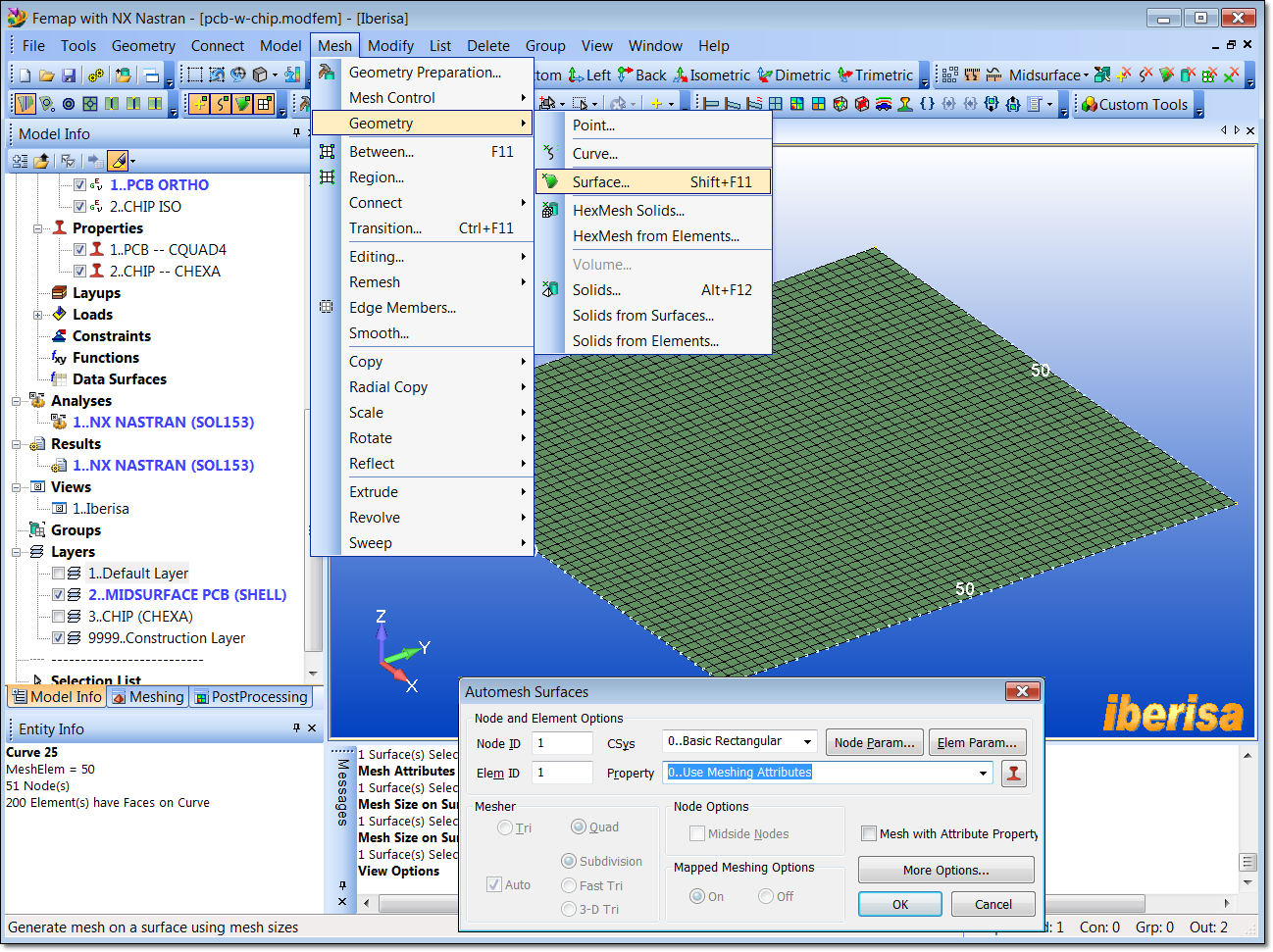
Meshing the PCB with 2-D Plate CQUAD4 elements

 

9. Create a 3-D Solid Mesh for the CHIP
First at all let's create a new LAYER where to isolate both the 3-D solid geometry and 3-D solid mesh for the CHIP. Simply click on "MODIFY > LAYER > SOLID" and create the new layer named for instance "CHIP (CHEXA)". After moving geometry to CHIP layer regenerate the screen using "Ctrl-G" and make sure that is active doing a double-click on the layer.


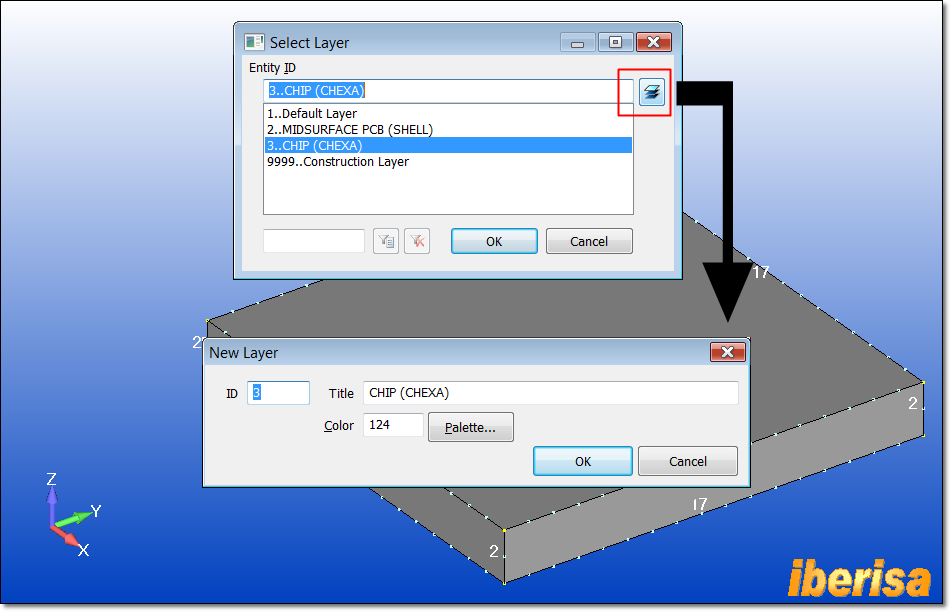
Moving the CHIP to a new layer

 

Secondly, let's prescribe meshing attributes to the 3-D Solid geometry for the CHIP using "Mesh > Mesh Control > Attributes On Solid" and click on the CHIP solid. In the "Select Mesh Property" form browse and select the correct solid property for the CHIP:


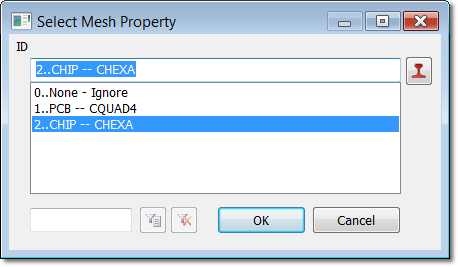
Prescribing Mesh Attributes to CHIP to mesh with 3-D Solid CHEXA 8-nodes elements

 

Third, let's prescribe Mesh Sizing attributes to the faces of the solid using "Mesh > Mesh Control > Mesh Size On Surface > Method => On Solid" and click on the solid CHIP. In the "Automatic Mesh Sizing > Element Size" field enter a value of 3/2, this will prescribe 2 divisions along the solid thickness of the CHIP of full dimensions 25x25x3 mm.


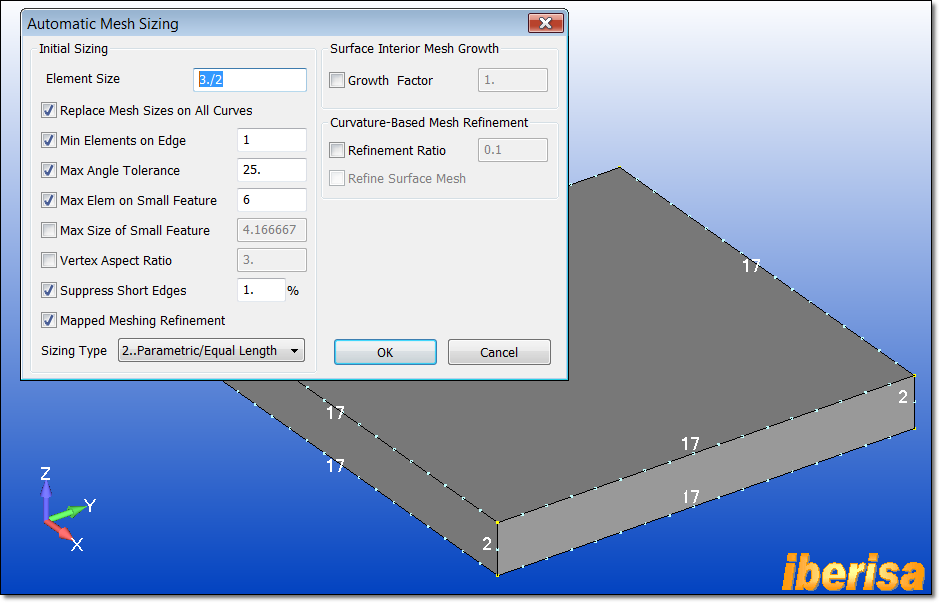
Prescribing Mesh Size to CHIP to mesh with 3-D Solid CHEXA 8-nodes elements

 

And finally mesh the CHIP body with 3-D hexaedral CHEXA elements using "Mesh > Geometry > HexMesh Solids" and click on the CHIP. In the "Hex Mesh Solids > Property" field make sure that appear the option "0..Use Meshing Attributes", this means that you have done the job correctly prescribing meshing properties to the geometry, if not please repeat the steps above.


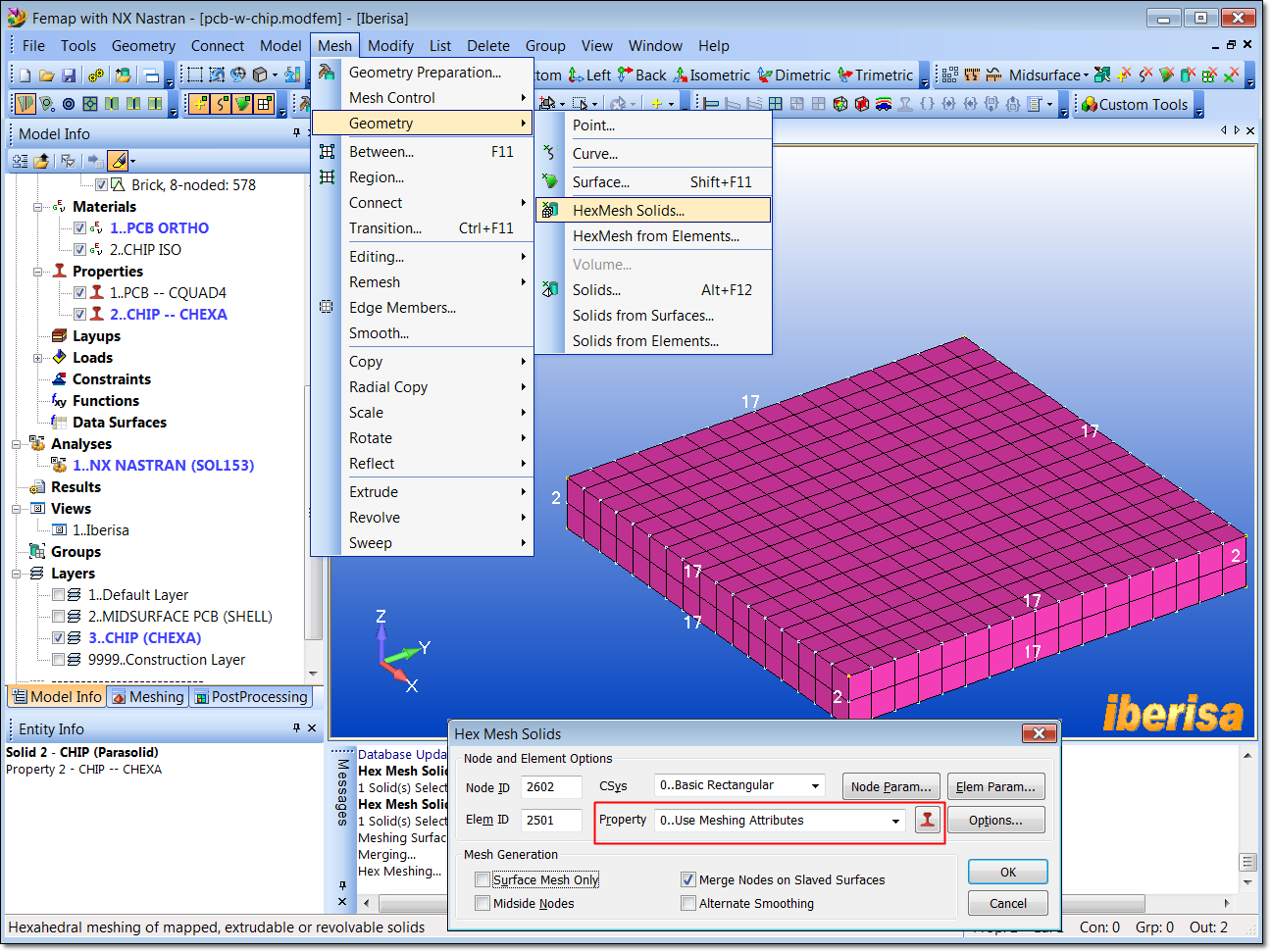
CHIP meshed with 3-D Solid CHEXA 8-nodes elements

 

10. Create a Heat load
A heat load defines the power or energy per time applied into the selected geometry.
Let´s apply a 5 W heat load to the top surface of the chip using command "Model > Load > On Surface" and select Heat Flux in the list of loads.


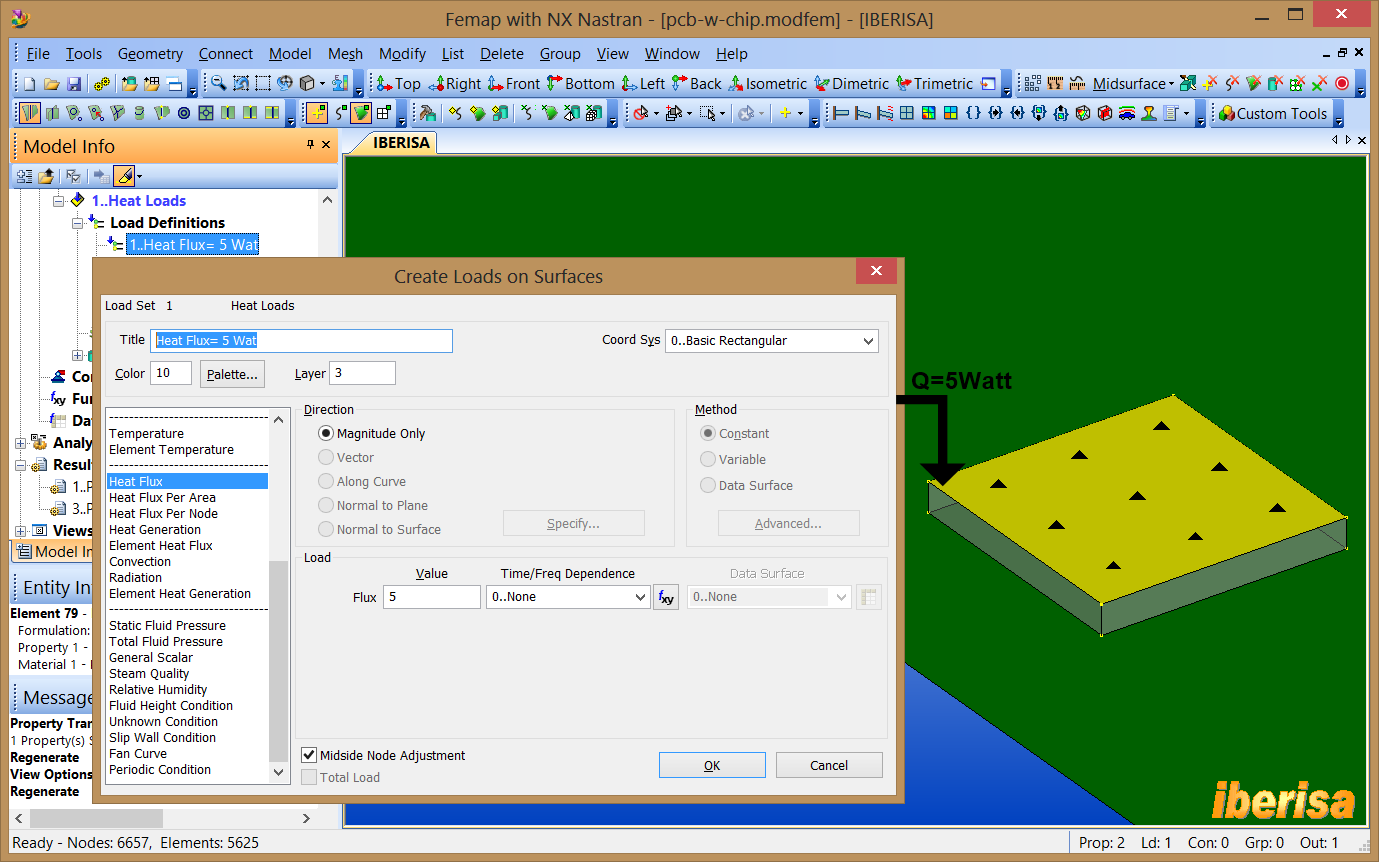
Applying a Heat Load to top surface of the CHIP

 

11. Create a Temperature Constraint
A temperature constraint defines known temperatures of a heat source or heat sink within the thermal model.
Let's apply a temperature constraint of 25°C to the edge of the PCB opposite to the edge closest to the chip using command "Model > Load > On Curve" and select Temperature in the list of loads.


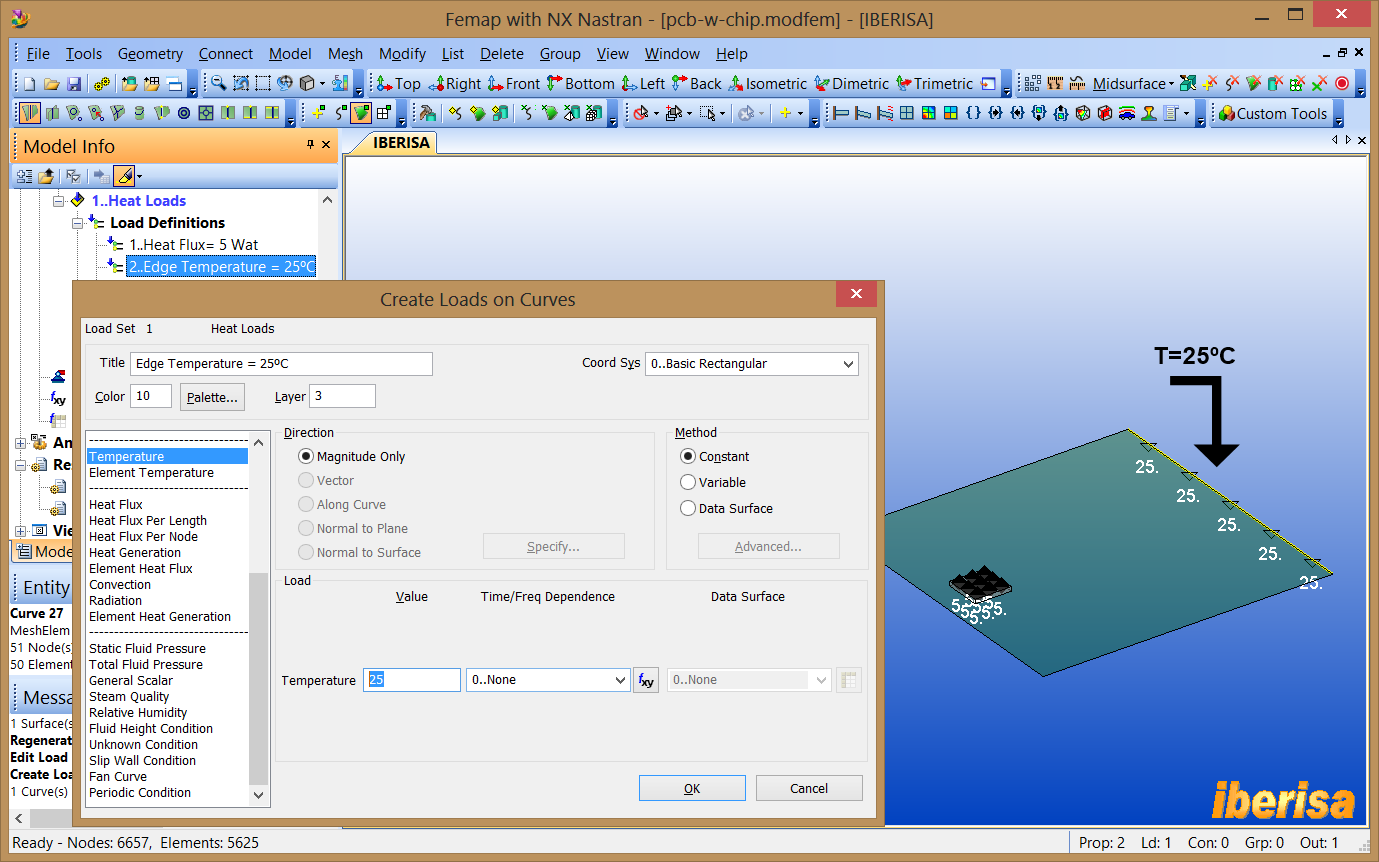
Applying a Temperature Constraint to the edge of PCB

 

12. Create a Convection Constraint for the CHIP
A convection constraint simulates convection for one or more surfaces by implicitly modeling the movement of fluid at a specific temperature in contact with one or more surfaces. In this case assume that the convection coefficient on the top and side faces of the chip is averaged to a single value of h = 24 W/m2ºC = 24e-6 W/mm2ºC, being 30ºC the ambient temperature of the fluid around the chip. Use command "Model > Load > On Surface" and select Convection in the list of loads. Select the TOP face as well as the four SIDE faces of the CHIP.


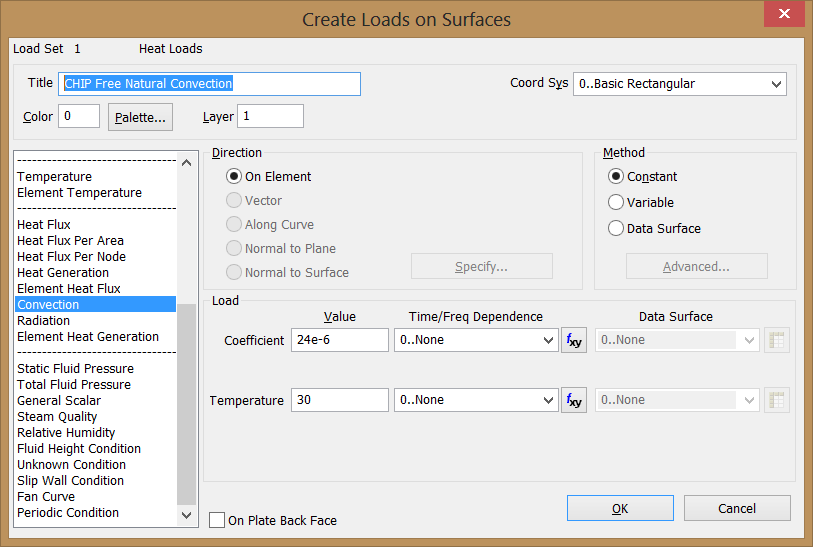
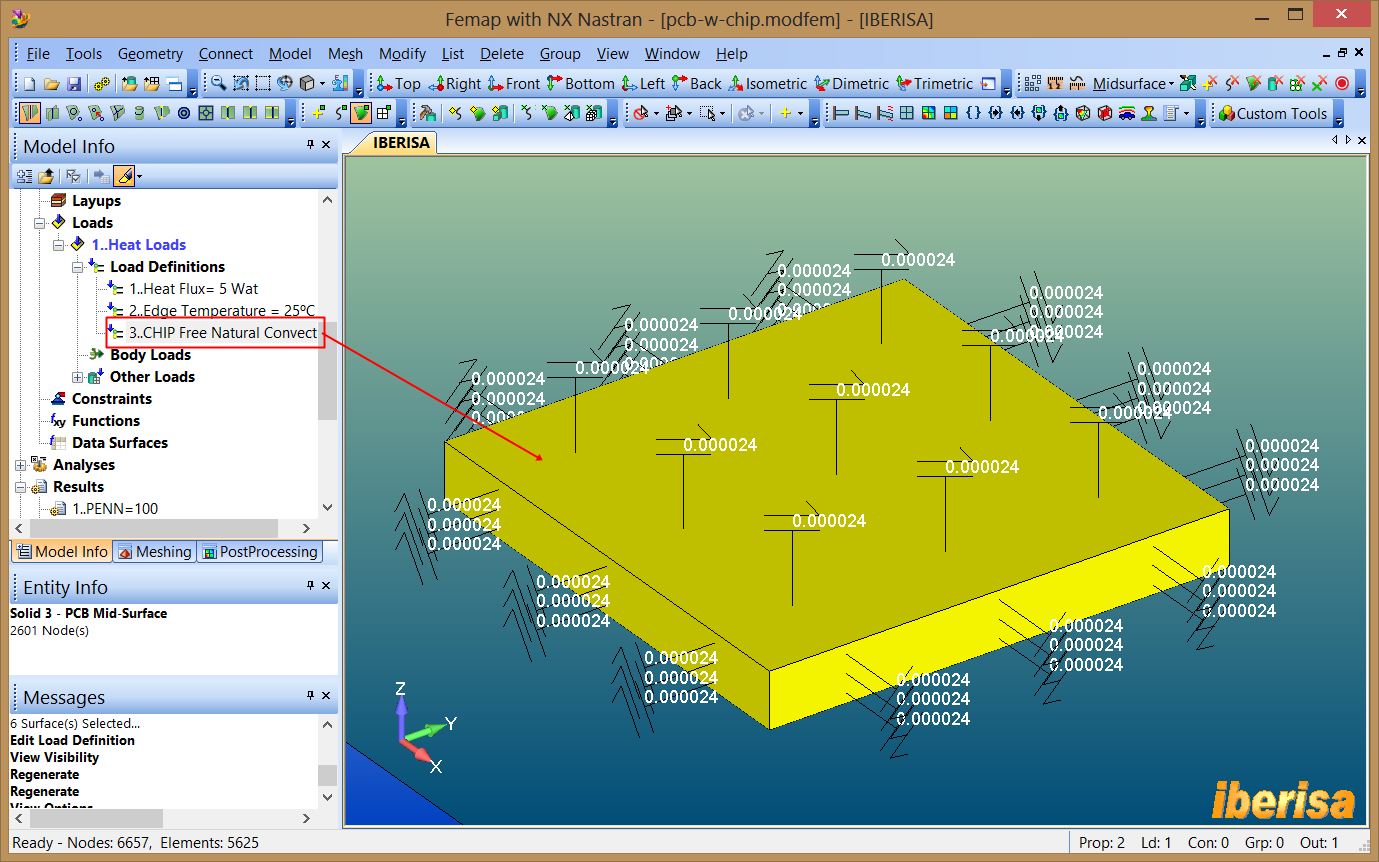
Applying a Convection Constraint to the CHIP

 

13. Create a Convection Constraint for the PCB
A convection constraint to the top face of the PCB with a lower heat transfer coefficient of 19 W/m2ºC = 19e-6 W/mm2ºC, being 25ºC the ambient temperature of the surrounding fluid. Use command "Model > Load > On Surface" and select Convection in the list of loads. Select the TOP face of the PCB.


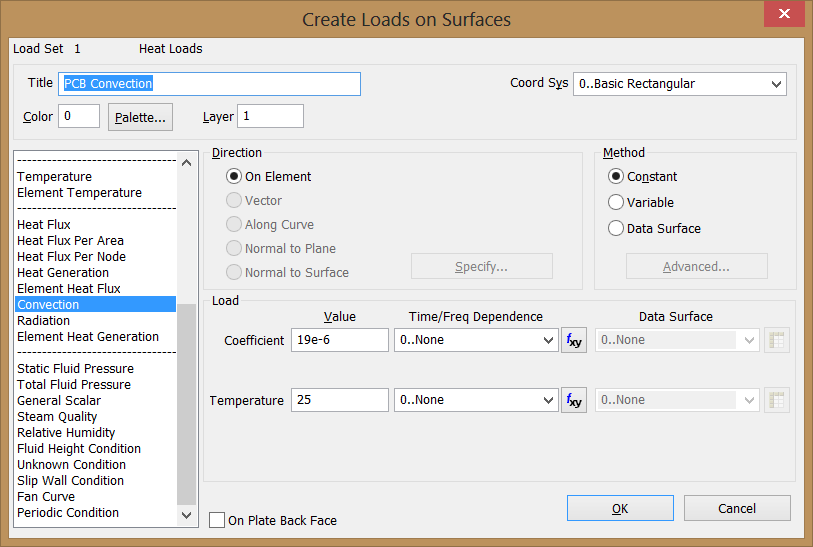
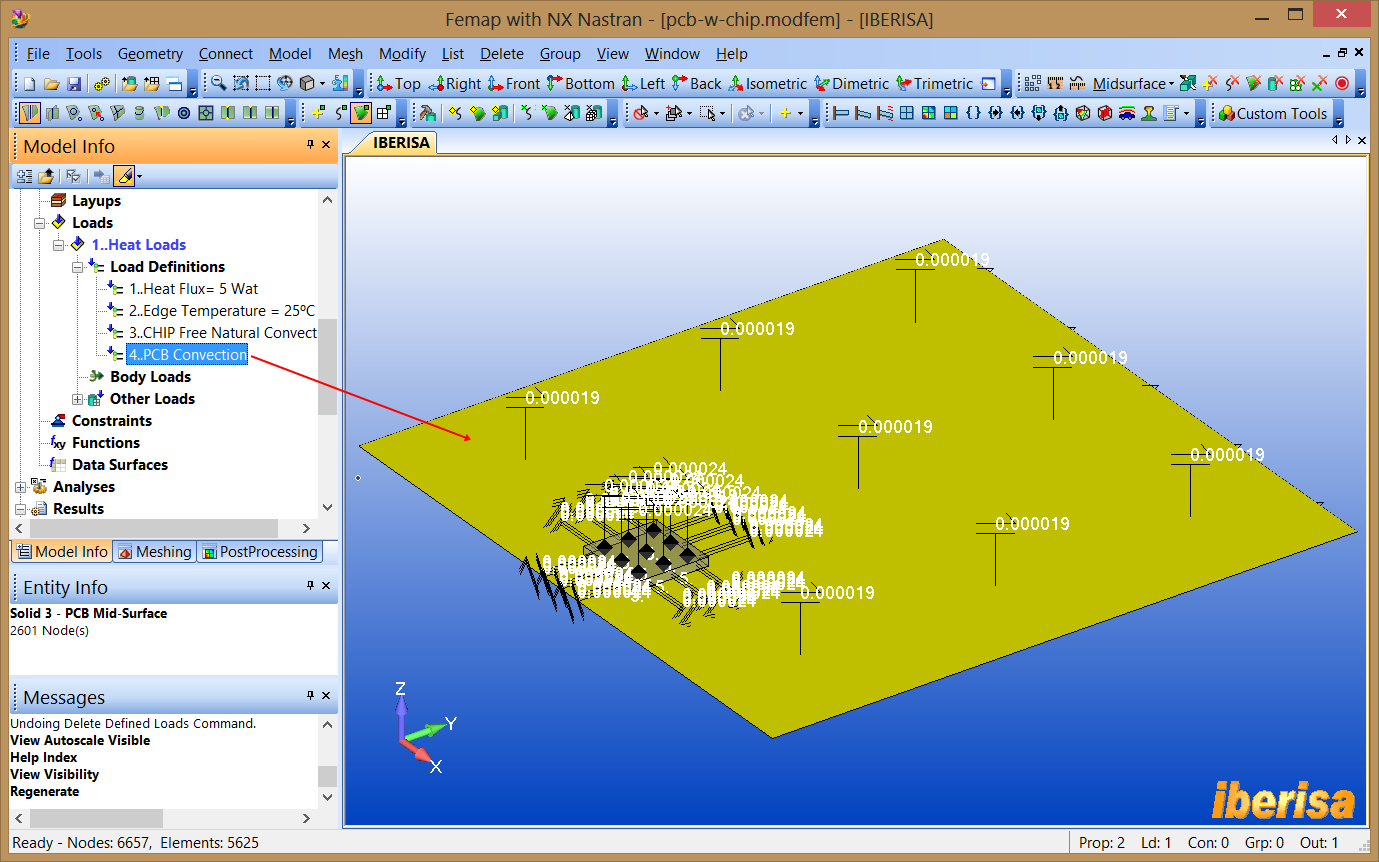
Applying a Convection Constraint to the PCB

 

14. Create the Contact Thermal Coupling
A thermal coupling models conduction between the entities of components that are physically or thermally in contact, like in this case CHIP & PCB. First let's explain the most important aspects that are behind the glue contact algorithm used by NX NASTRAN.

Element Gluing

An option to glue elements together during a solution is available in NX Nastran. Glue is a simple and effective method to join meshes which are dissimilar. It correctly transfers displacement and loads resulting in an accurate strain and stress condition at the interface. The grid points on glued edges and surfaces do not need to be coincident.

Glue creates stiff springs or a weld like connection to prevent relative motion in all directions. For discussion purposes, the internal elements created by the solver from glue definitions will be referred to as “glue elements” in the documentation.

The following table summarizes all supported glue conditions:

Type

Description

Solution Support

Edge-to-Edge

Glue between the edges of shell, axisymmetric, plane stress, and plane strain elements.

All solutions except SOLs 144 -146, 601 and 701

Edge-to-Surface

Glue between shell element edges and shell or solid element faces

All solutions except SOLs 144 -146, 601 and 701

Surface-to-Surface

Glue between shell or solid element faces and shell or solid element faces

All solutions except SOLs 144–146, and 701

Defining Glue Conditions

Select the glue property.
Define source and target regions.
Pair the source and target regions.
Optionally adjust the glue algorithm using glue control parameters.
Optionally request glue surface traction output.

Surface-to-Surface Glue Summary

Surface-to-surface glue can be defined on the faces of the following elements.

Shell elements CTRIA3, CTRIA6, CTRIAR, CQUAD4, CQUAD8, and CQUADR.
Solid elements CHEXA, CPENTA, CPYRAM, and CTETRA.

You create shell or solid element face regions with the BSURF, BSURFS, BCPROP, or BCPROPS bulk entries. You then pair the regions using the source and target fields on the BGSET bulk entry. From elements in the source region, a top and bottom normal is projected. The software creates a glue element if:

Any of the source element normals intersect with an element in the target region.
The distance between the two faces is equal to or less than the search distance in which you specify for the glue pair.

Surface-to-surface glue definitions are supported in all solution sequences except for SOL 144–146, and 701. In the heat transfer solutions 153 and 159, they are treated as conductivity connections. Surface-to-surface glue connections can also be defined between acoustic mesh faces.

GLUE Control Parameters

The glue control parameters on the BGPARM bulk entry (optional) can help you adjust the glue algorithm. Please note that for Heat Transfer Analysis (SOL153/159) NX NASTRAN always uses GLUETYPE=1, with unique penalty factor inputs. The DEFAULT values defines a PERFECT GLUE contact condition, ie, in Heat Transfer Analysis a perfect conductivity between coupled entities, but if you require to TUNE the thermal coupling then you will need to "play" with the different glue control parameters of BGPARM entry (see NX NASTRAN QUICK REFERENCE GUIDE, Remark#2 of BGPARM entry)

GLUETYPE=1

The glue penalty stiffness is defined by PENN and PENT.
(Solutions 153 and 159 - Heat transfer analysis always uses GLUETYPE=1)
 

PENTYP=1

Structural solutions: PENN and PENT have units of 1/(length), and the glue element stiffness is calculated by K = e*E*dA where e represents PENN or PENT, E is an average modulus (averaged over elements associated with the source side region), and dA is area. A physical interpretation is that it is equivalent to the axial stiffness of a rod with area dA, modulus E, and length 1/e.

Solutions 153 and 159: PENT is ignored. PENN has the units of 1/(length), and “conductance” at the glue connection is calculated as C = e*kavg*dA, where e represents PENN, kavg is an average of the thermal conductivity (k) values for all source side elements in a pair, and dA is area. A physical interpretation is that it is equivalent to the axial "conductance" of a rod with area dA, conductivity kavg, and length 1/e.

PENTYP=2

Structural solutions: PENN and PENT become a spring rate per area Force/(Length x Area), and the glue element stiffness is calculated as K=e*dA. The spring rate input is a more explicit way of entering glue stiffness since it is not dependent on the average modulus.

Solutions 153 and 159: PENT is ignored. PENN has the units of (thermal conductivity*length)/area, and the “conductance” at the glue connection is calculated as C = e*dA. Another term for e is heat flux.

 

To define de Control Parameters of the GLUE Thermal Coupling of BGPARM entry in FEMAP use the command "Connect > Connection Property".

In a Heat Transfer Analysis model (SOL153/159) if the user do not specify any particular conductance for the glue contact, then NX Nastran will use the defaults values of GLUETYPE=1, PENTYP=1 and PENN=100. Per BGPARM Remark 2, the conductance of the glue is e*kavg*dA, where e is PENN (100) and kavg is the average thermal conductivity of all of the materials in the model. Then for the original MAT5 materials, the three diagonal values are used in the average, therefore, kavg for the entire model is kavg = (0.383 + 0.009 + 0.041 + 0.00055)/4 = 0.10838 W/mmºC. Multiplied by e (PENN), this is e* kavg = 100*0.10838 = 10.838 W/mm2ºC, which is almost 300 times bigger of the target value (The exact ratio is 10.838/0.04 = 270).


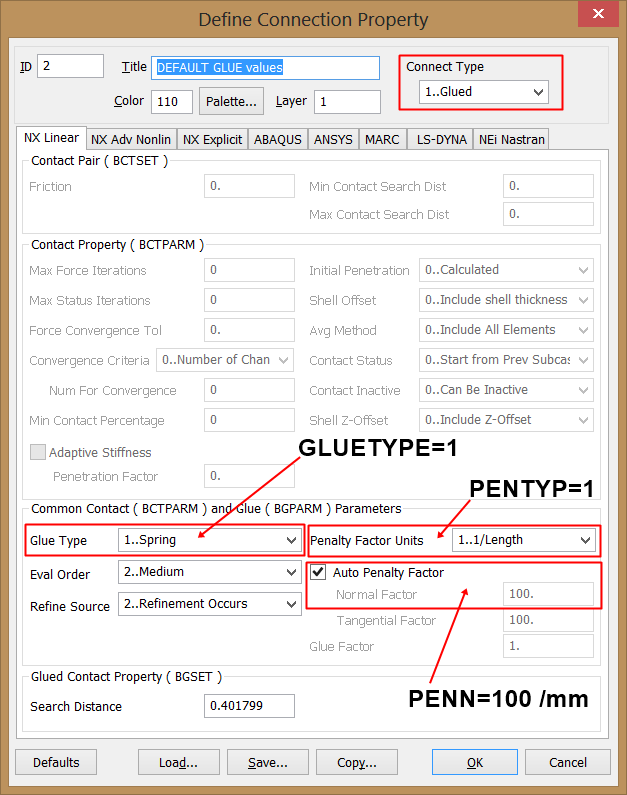
GLUE Thermal Coupling DEFAULT VALUES

 

For simplicity, I suggest to use always GLUETYPE=1 and PENTYP=2, which allows you to directly specify the conductance via PENN, having the units of (Thermal Conductivity*Length)/Area. Thermal Conductivity in SI has units of W/mºC, thus PENN has units of W/mm2ºC, i.e., directly the value of the Heat Transfer Coefficient of the Thermal Coupling.

The PENN value is independant of the GLUE surface area, the user does not need to know the glue surface area by advance, this value is computed by the glue algorithm and is a function of the mesh size/shape, glue refinement, etc..

So, setting "Glue Type = 1..Spring" (GLUETYPE=1), also "Penalty Factor Units = 2...Force/(Length x Area)" (PENTYP=2) and "Normal Factor = 0.04" W/mm2ºC (PENN), the definition of GLUE Thermal Coupling parameters will be correct as shows the following image:


GLUE Thermal Coupling using GLUETYPE=1, PENTYP=2 and PENN = Heat Transfer Coeff. Value

 

Definition of Thermal Coupling

The command "Connect > Surfaces" allows simple creation of a “connection” between two single surfaces, a set of surfaces and a single surface, or two sets of surfaces. Basically, it allows you to create 2 separate Connection Regions then automatically creates a Connector between those Connection Regions using a specified Connection Property.

Target Region: select the midsurface of the PCB as TARGET.

Source Region: select the BOTTOM SIDE of the CHIP as SOURCE.

Connection Property: select the existing Connection Property to use when creating this connection.


Creation of GLUE Thermal Coupling between CHIP & PCB

 

You can edit the definition of any region or connector pair using the command "Modify > Edit > Region" or "Modify > Edit > Connector", or simply clik with the right mouse button (RMB) on the MODEL INFO TREE on top of any command and take advance of the many options of the unfolded menus.


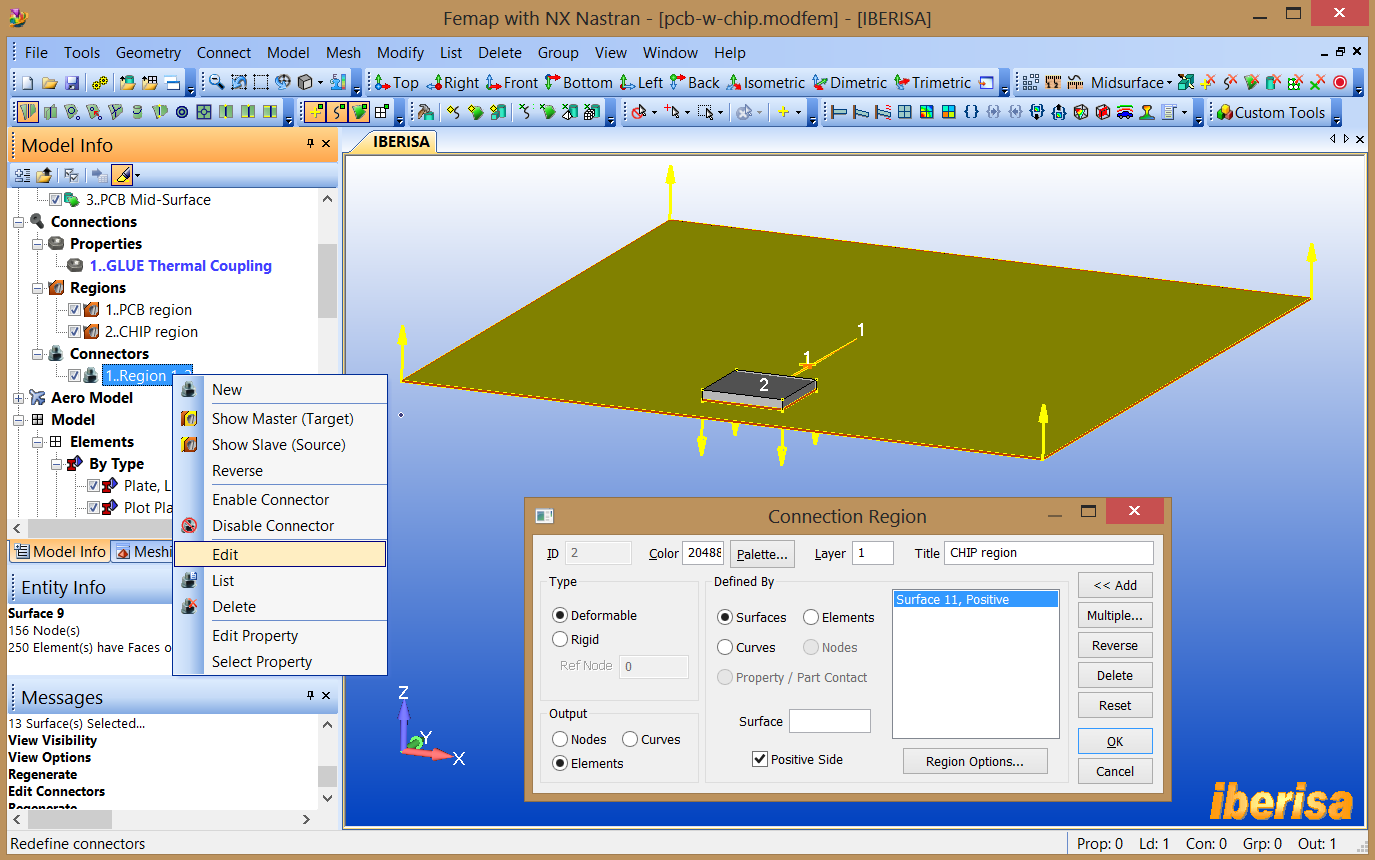
Editing entities using unfolded menus of the MODEL INFO TREE

 

15. Material Orientation of the PCB
Please remember that NX NASTRAN requires to align explicitely the principal directions of a non-isotropic material. Whenever using orthotropic or anisotropic materials, defining a material angle for all of planar elements should by done previously to launching the solver for analysis. Use command "Modify > Update Elements > Material Orientation > Method => Property" and select any element of the PCB.


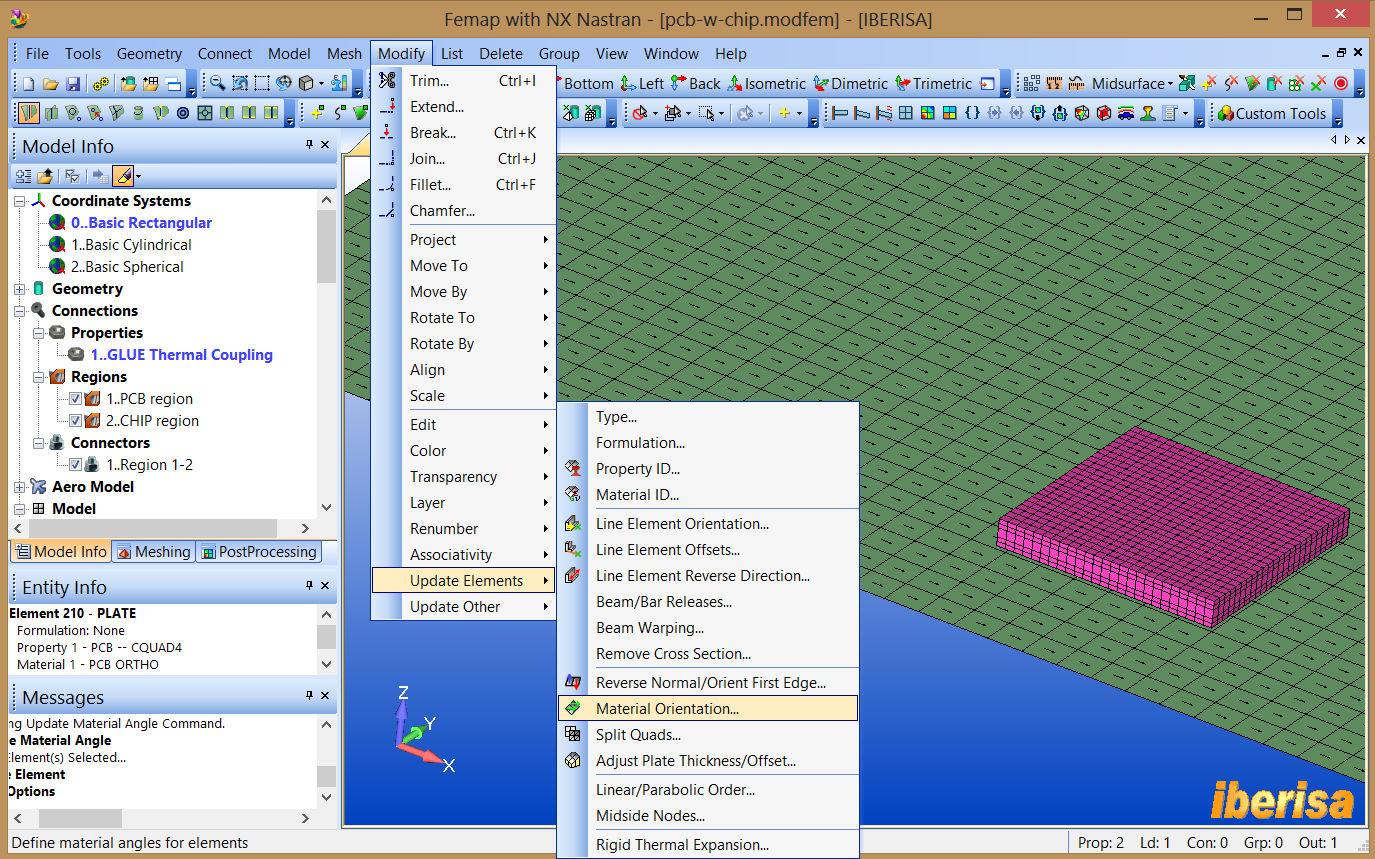
Definition of Material Orientation for Orthotropic material of PCB

 

In the field "Material Coordinate System" select "X Axis of CSys" and click OK. This is mandatory to use with NX Nastran solver, then FEMAP will write out a “Material Coordinate System ID” (MCID) for each element instead of a material angle (THETA). The X-direction of the selected coordinate system is always used and this moves calculation of the material angle from FEMAP to the solver.


Definition of Material Coordinate System

 

Viewing Material Angles

The defined material angles for planar elements may be viewed using the "View > Options" command (click F6 and you are done!). Choose the "Element - Material Direction" and turn on "Show Material Direction". This will display a small vector at the center of each element where an angle has been defined. The orientation of the vector shows the specified angle. Typically, all of the vectors should be parallel - then elements are known to be properly aligned.


How to View Material Direction

 

16. Create the Steady-State Thermal Analysis and Solve the Model
Create an analysis set for Steady-State Heat Transfer using the FEMAP Analysis Set Manager from command "Model > Analysis". Select “36..NX Nastran” from the Analysis Program drop-down list, then select “20..Steady-State Heat Transfer” from the Analysis Type drop-down list. Click OK, and in the Analysis Set Manager dialog box click Analyze.


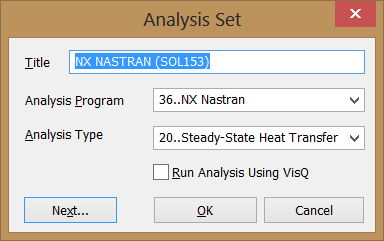
Definition of Steady-State Heat Transfer Analysis

 

17. Postprocessing the Thermal Results
You can see the effects of the orthotropic material in the temperature distribution. Heat is better conducted in the Y direction. Temperatures vary from approximately 25 ºC to 60 ºC.


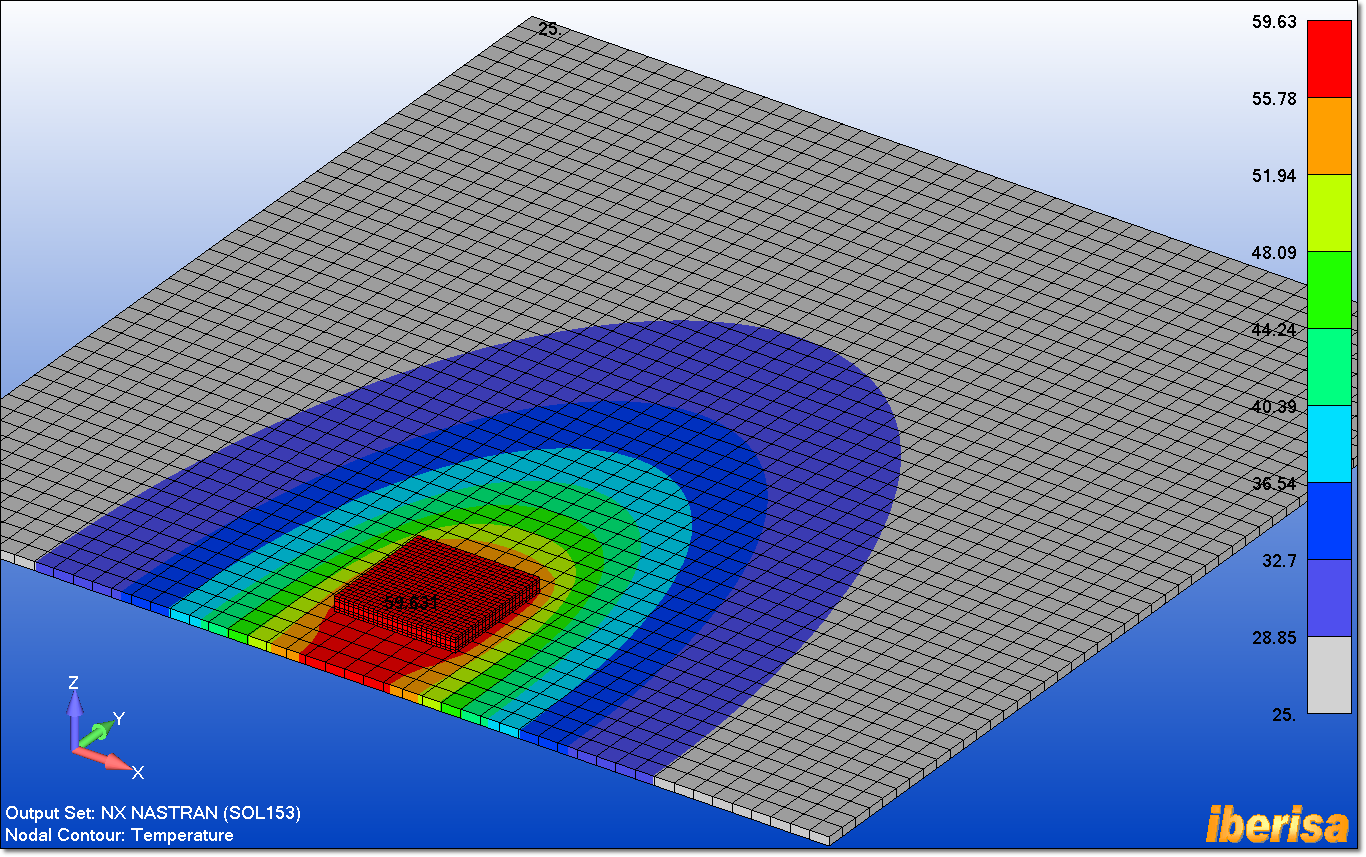
Temperature Distribution (ºC) in the full model

 

18. Display the Temperature Gradient in the CHIP
Click on PROPERTIES and select GROUP to make automatically a group of elements for each poperty, this way we will be able to postprocess results separately either in PISTON or PCB. In the MODEL INFO TREE double-click on Group "2.. Property 2 - CHIP", then click on GROUPS and select "Show Active Group", you will observe the temperature variation on the chip corresponding to value limits shown on the color bar between 58.7ºC and 59.6ºC.


Temperature Distribution (ºC) in the CHIP

 

This concludes the Chip & Printed Circuit Board Heat Transfer Analysis example using GLUE Surface-to-Surface Thermal Coupling feature and Orthotropic material properties, I hope to be helpful and useful.

Best regards,
Blas.

 


SÍGUENOS EN: Blog de "FEMAP y NX Nastran" en WordPress

Ir a la Página de Inicio

Productos | Soporte | Consultoría | Cursos | Universidad | Libros | Enlaces
Copyright © 2001 Ibérica de Ingeniería, Simulación y Análisis, S.L. -- http://www.iberisa.com --