
Introducción al Análisis de Fatiga o Durabilidad
En la vida real se observa que repetidos ciclos de carga y descarga debilitan las piezas a lo largo del tiempo incluso cuando las cargas inducidas están considerablemente por debajo de la tensión de rotura estática e incluso del límite elástico del material. Este fenómeno se le conoce como Fatiga. Cada ciclo de fluctuación de la tensión deteriora o daña la pieza un poco. Tras un nº de ciclos determinado, la pieza está tan debilitada que rompe por Fatiga. Para complicar el tema también se observa en piezas metálicas que por debajo de un cierto valor de la tensión no se produce la rotura por elevado que sea el nº de ciclos de trabajo de la pieza. Todo esto hace que la Fatiga sea realmente compleja y por desgracia para el ingeniero de diseño una de las primeras causas de fallo en muchas piezas construidas con materiales férricos. Ejemplos de fallo por fatiga los tenemos en máquinas rotativas, tornillos, alas de aviones, productos de consumo, ruedas de ferrocarril, plataformas marítimas, barcos, vehículos y puentes.
La vida a fatiga se puede definir como el "fallo debido a cargas repetitivas ... que incluye la iniciación y propagación de una grieta o conjunto de grietas hasta el fallo final por fractura" (Fuchs, 1980). El análisis de fatiga estructural es una herramienta para evaluar la validez de un diseño, o su durabilidad, bajo condiciones de carga simples o complejas conocidas como cargas de servicio. Los resultados del análisis de fatiga se representan mediante contornos en color que muestran la duración de los ciclos de carga que la estructura puede soportar antes de que se inicie cualquier grieta.
Los estudios estructurales lineales y no lineales no predicen los fallos por fatiga. Calculan la respuesta de un diseño sujeto a un entorno específico de cargas y restricciones. Si los resultados de desplazamientos y tensiones están por debajo de un cierto nivel admisible el ingeniero proyectista puede concluir que el diseño es seguro en ese entorno de solicitaciones con independencia de cuantas veces se aplique la carga.
Los resultados de los estudios estructurales (estáticos y dinámicos, lineales y no lineales) se usan como los datos básicos de partida para definir el estudio de fatiga. El nº de ciclos requeridos para que el fallo por fatiga ocurra en un punto depende del material y de la fluctuación de las tensiones. Esta información, para ciertos tipos de materiales férricos, nos la proporciona la llamada Curva S-N.
Las grietas por Fatiga se inician en la superficie del material. Por ello debe evitarse en lo posible ralladuras y arañazos en las superficies de buen acabado (por ejemplo, grabar el nombre comercial en la pieza), sobre todo en zonas con elevado nivel de tensión. Cualquier tratamiento superficial (térmico o mecánico) que produzcan un estado de tensiones residuales de compresión en la superficie de las piezas aumentando la dureza de la superficie (por ejemplo, el temple, granallado o laminado superficial) incrementará la vida a fatiga de la pieza.
El análisis de fatiga se basa en la regla de Miner de daño acumulado para estimar la vida a fatiga a partir de una historia de tensiones o deformaciones. La estimación se realiza reduciendo los datos de carga a una secuencia de picos y valles, contando los ciclos y calculando la vida a fatiga. Para realizar un análisis a Fatiga o de durabilidad, se debe proporcionar información específica para el análisis de fatiga:
Propiedades a fatiga de los materiales |
|
Variación de las cargas a fatiga |
|
Opciones de análisis a fatiga |
Fases de
un Fallo por Fatiga

Los fallos por Fatiga se producen en tres fases:
Fase 1 (Iniciación): Una o más grietas se desarrollan en el material. Las grietas pueden aparecer en cualquier punto del material pero en general ocurren alrededor de alguna fuente de concentración de tensión y en la superficie exterior donde las fluctuaciones de tensión son más elevadas. Las grietas pueden aparecer por muchas razones: imperfecciones en la estructura microscópica del material, ralladuras, arañazos, muescas y entallas causados por las herramientas de fabricación o medios de manipulación. En materiales frágiles el inicio de grieta puede producirse por defectos del material (poros e inclusiones) y discontinuidades geométricas. |
|
Fase 2 (Propagación): Alguna o todas las grietas crecen por efecto de las cargas. Además, las grietas generalmente son finas y de difícil detección, aun cuando se encuentren próximas a producir la rotura de la pieza. |
|
Fase 3 (Rotura): La pieza continúa deteriorándose por el crecimiento de la grieta quedando tan reducida la sección neta de la pieza que es incapaz de resistir la carga desde un punto de vista estático produciéndose la rotura por fatiga. |
Curva S-N

La Curva S-N de un material define valores de tensiones alternas vs. el nº de ciclos requeridos para causar el fallo a un determinado ratio de tensión. La siguiente figura muestra una curva típica S-N. El eje-Y representa la tensión alterna (S) y el eje-X representa el nº de ciclos (N). La curva S-N se basa en un ratio de tensión o tensión media smm. Para cada material se pueden definir múltiples curvas S-N con diferentes valores de tensión media.
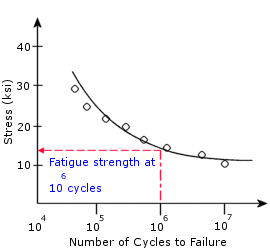
Las curvas S-N se basan en la vida a fatiga media o en una probabilidad de fallo dada. La generación de la curva S-N de un material requiere muchos ensayos para de una forma estadística variar las tensiones alternas, las tensiones medias (o ratio de tensión) y contar el nº de ciclos. Para caracterizar un material se toma un conjunto de probetas y se las somete a solicitaciones variables con diferentes niveles de tensión, contándose el nº de ciclos que resiste hasta la rotura. Debido a la elevada dispersión estadística propia de la fatiga los resultados se agrupan en una banda de roturas. Una parte de esta dispersión puede atribuirse a errores del ensayo, pero es una propiedad del fenómeno físico lo cual obliga a realizar un gran nº de ensayos de probetas a fin de determinar la banda de fractura con suficiente precisión. Por tanto, caracterizar un material a fatiga supone un coste muy importante.
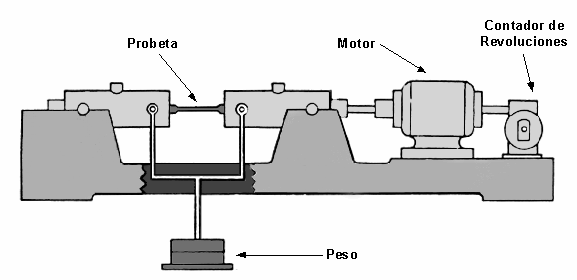
Máquina de probeta rotatoria de Moore para ensayo a Fatiga
Por ejemplo, supóngase que se desea conocer el comportamiento a fatiga de un material hasta 1e8 ciclos utilizando seis valores de la tensión con tres probetas por cada tensión. El ensayo más largo de 1e8 ciclos costaría unos 14 días en una máquina capaz de producir 5000 ciclos/min. Por tanto si sólo se dispone de una máquina el tiempo para realizar todos los ensayos sería de varios meses. Existen métodos de ensayo rápidos pero la fiabilidad de los resultados es menor.
En base a los ensayos sobre probetas se han desarrollado métodos para cálculo y diseño a Fatiga. La extrapolación de los resultados de los ensayos de fatiga a las piezas reales está basado en la utilización de una serie de valores modificativos empíricos, y por ello la fiabilidad de los métodos de cálculo es reducida si se compara por ejemplo con un cálculo estático lineal ya que existen numerosos factores que intervienen en el comportamiento a fatiga de un sistema físico que son imposibles de introducir en un modelo de elementos finitos, teniendo el usuario que "estimar" su efecto. Por tanto, en sistemas de alta responsabilidad es imprescindible recurrir a ensayos sobre prototipos.
Limitaciones del Análisis de
Fatiga

Los fundamentos para la predicción de vida a fatiga se basan en las propiedades del material obtenidas en el laboratorio ensayando con pequeños especímenes sujetos a cargas dinámicas hasta que parten o aparece la primera grieta. El método de tensión-deformación local asume que la vida del especímen en el laboratorio se puede relacionar con la vida de la estructura real. Es más, se asume que las cargas utilizadas en la estimación de vida a fatiga de la estructura son tensiones locales o deformaciones locales en posiciones críticas.
Dado que los fundamentos del análisis de fatiga están basados en datos empíricos, considerar los siguientes puntos antes de realizar un análisis de fatiga:
Si se utilizan propiedades del material publicados en tablas, debe tenerse en cuenta las condiciones del ensayo utilizadas para obtener esos datos. Asegúrese de que las condiciones corresponden al problema que se está investigando, y que se incluyen los procesos utilizados para la fabricación del material y las mismas condiciones de carga del ensayo. |
|
Verificar la validez de las cargas y su aplicación correcta. |
Aparte de estas limitaciones, el análisis de fatiga es muy interesante, especialmente si se utiliza como una herramienta para ver características y tendencias de un posible fallo a fatiga. Modificando parámetros y comparando estimaciones de vida, se pueden observar tendencias a favor de un diseño más seguro. Únicamente a través de estudios comparativos el ingeniero podrá obtener un conocimiento real de los mecanismos de trabajo.
Las siguientes figuras ilustra los conceptos básicos de las cargas de fatiga junto con el significado de los símbolos utilizados en el análisis de fatiga:
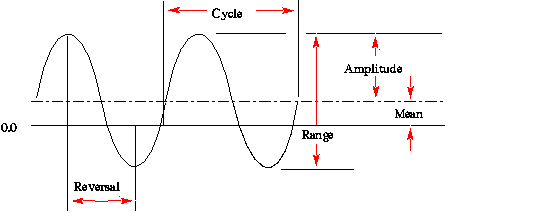

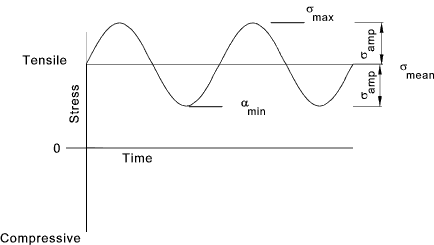
| Tensión máxima = smax | |
| Tensión mínima = smin | |
| Tensión media = smean = ( smax + smin )/2 | |
| Tensión variable (o tensión alterna, o amplitud de tensión, sr) = samp = ( smax - smin )/2 | |
| Rango de tensiones Ds = smax - smin | |
| Razón de tensiones (stress Ratio) R = smin / smax | |
| Razón de amplitud A = samp / smean |
Datos de Entrada

Las estimaciones de vida a fatiga se pueden generar para cualquier estructura en diseño. Primero se crea un histórico de tensiones que predice las cargas que la estructura va a soportar. La forma de la curva es muy regular.
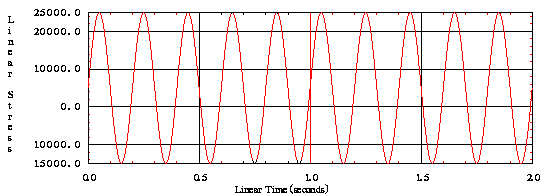
Una vez construido un prototipo de la estructura se le somete a un ensayo de fatiga con cargas hasta la rotura, o hasta alcanzar un nº de ciclos elevado. También se pueden colocar galgas extensométricas un puntos singulares denominados "hot spot" para generar historias de deformaciones unitarias. La curva de históricos de deformaciones unitarias es muy aleatoria, tal como muestra la siguiente figura:
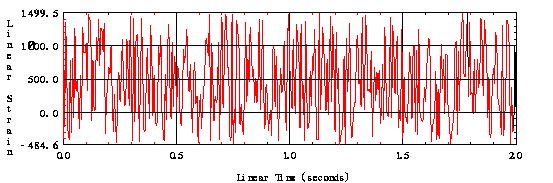
Estimación de Vida a Fatiga a
partir de Datos Experimentales

El proceso de estimación de vida a fatiga a partir de datos obtenidos experimentalmente se puede separar en tres pasos:
Reducción a picos/valles |
|
Conteo de ciclos |
|
Estimación de Vida |
Reducción a Picos/Valles

El proceso de reducción a picos/valles permite eliminar datos que tienen poco o ningún efecto en la predicción de vida a fatiga. No todos los puntos tienen interés para el análisis de fatiga, sólo los valores máximos (picos) y mínimos (valles) lo tienen, pero no la forma en que varía la tensión o deformación unitaria entre un par pico/valle. Para empezar, todos los puntos intermedios entre picos y valles se eliminan, tal como muestra la figura siguiente. Esto deja únicamente la curva con los puntos correspondientes a picos/valles.
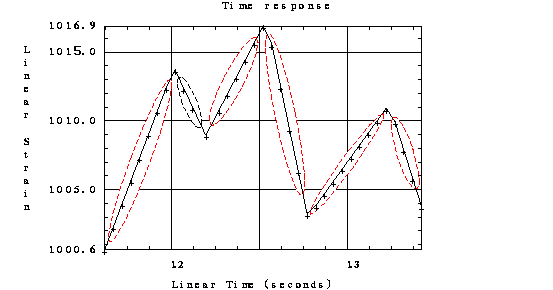
Seguidamente se eliminan los pares de puntos pico/valle que son insignificantes. Hay varias formas de hacerlo, una es especificar una tolerancia y eliminar pares pico/valle con una diferencia menor que la tolerancia. Por ejemplo, si en la siguiente figura se utiliza una tolerancia de 150 microstrains entonces los puntos 2 y 3, así como los puntos 5 y 6 se eliminan de la curva ya que el rango de deformación de ambos pares es 100, menor que 150.
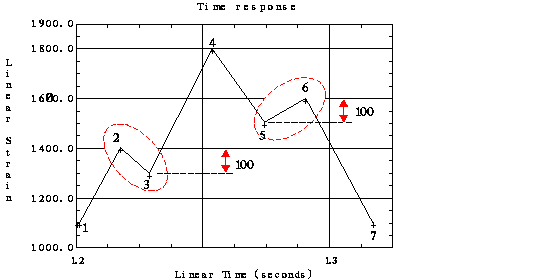
Cómputo de Ciclos

Tras reducir los datos de entrada a una secuencia de picos/valles se pasa a contar los ciclos. Si los datos se hubieran generado analíticamente, entonces los ciclos y sus correspondientes rangos de puntos se pueden determinar mediante inspección visual. Pero encontrar ciclos a partir de curvas de datos experimentales no es sencillo. Se han empleado muchos años de investigación en esta materia resultando en una variedad de algoritmos de cómputo de ciclos a partir de datos experimentales.
Un cambio de pendiente es medio ciclo, y una amplitud es medio rango. Cuando se "cuenta" un ciclo, puede que en efecto se haya encontrado un cambio de pendiente, dependiendo del algoritmo. Junto con cada ciclo o cambio de pendiente viene su correspondiente rango o amplitud.
Un simple método de contar ciclos es identificar cada sucesivo par pico/valle como un rango.
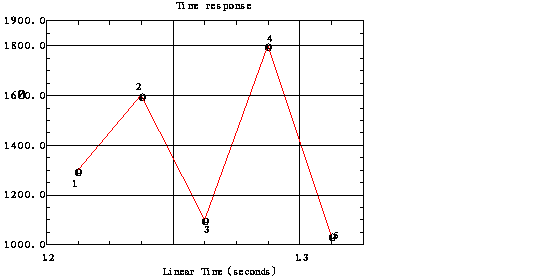
Para los datos de la curva anterior, los puntos 1-2, 2-3, 3-4, y 4-5 son todos rangos usando este método de conteo.
Entre los métodos de cómputo de ciclos los más importantes son los siguientes:
Range-pair |
|
Rainflow |
q Método Range-Pair
El algoritmo range-pair detecta un cambio de pendiente (y por tanto un rango) de dos casos diferentes:
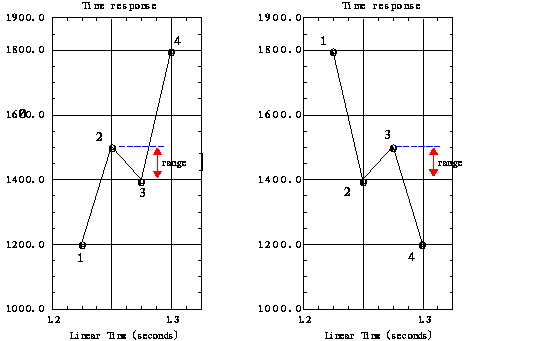
Para el rango de pendiente positiva, el punto 1 debe ser menor o igual al punto 3, y el punto 2 debe ser menor o igual que el punto 4. Para la serie de pendiente negativa, el punto 1 debe ser mayor o igual que el punto 3, y el punto 2 debe ser mayor o igual que el punto 4,
Cuando dos puntos se determina que forman un rango, se excluyen del conteo. En los ejemplos mostrados, los puntos 2 y 3 se eliminan del cómputo, mientras que los puntos 1 y 4 se volverán a usar de nuevo.
q Método Rainflow
El algoritmo de rainflow es el método de conteo más popular para la estimación de vida a fatiga porque sigue el bucle de histéresis de la curva tensión-deformación. Este método de conteo recibió el nombre de rainflow por sus creadores, M. Matsuishi y T. Endo, porque gráficamente se parece al agua de lluvia fluyendo por el techo de una pagoda
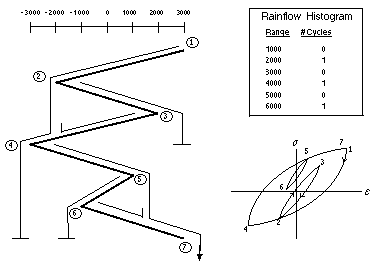
Las reglas que gobiernan el método rainflow son las siguientes:
Ordenar el histórico de forma que la mayor magnitud sea el primer pico y el último valle.
Empezando con el primer pico o valle, permitir que la lluvia gotee hasta que un ciclo se cierre, tal como se describe en el paso 3; o hasta que la lluvia se pare, tal como se describe en el paso 4.
Si se empieza en un pico, un ciclo se cierra cuando se encuentra otro pico cuyo valor es mayor o igual que el pico de inicio. Esto se demuestra con los puntos 5-6-7. Si se empieza en el punto 5, la lluvia cae hasta el punto 6 y seguidamente cae directamente al punto 7. Se para en el punto 7 porque la magnitud del punto 7 es mayor que el punto 5. Un ciclo se indica en la figura con una línea corta horizontal donde se para la lluvia.
Si se empieza en un valle, un ciclo se cierra cuando se encuentra un valle opuesto con un valor menor o igual al valle de arranque. Esto se demuestra con los puntos 2-3-4. Empezando por el punto 2, la lluvia cae hasta el punto 3, y luego gotea hasta el punto 4. Se para enfrente del punto 4 porque la magnitud del valle 4 es menor que el valle 2.
La lluvia se para cuando se encuentra con lluvia cayendo desde uno de los tejados anteriores. Esto se demuestra por la lluvia, que corre del punto 3 al punto 4. Se para antes de llegar al punto 4 por la lluvia cayendo del punto 2. La línea corta vertical al final de la línea corriendo desde 3 a 4 indica que la lluvia está parada.
Tras cerrar un ciclo, o que la lluvia esté parada para el primer punto, moverse al segundo punto y permitir que la lluvia caiga. Repetir ésto hasta que cada punto se haya procesado.
Estimación de Vida a Fatiga

Una vez realizado el cómputo de ciclos, se pasa a calcular el nº de ciclos para el fallo mediante una ecuación de estimación de vida a fatiga.
q Stress-Life
La ecuación de tensión-vida (stress-life) se lleva utilizando desde finales de 1800. Asume que el fallo ocurre tras un elevado número de ciclos.
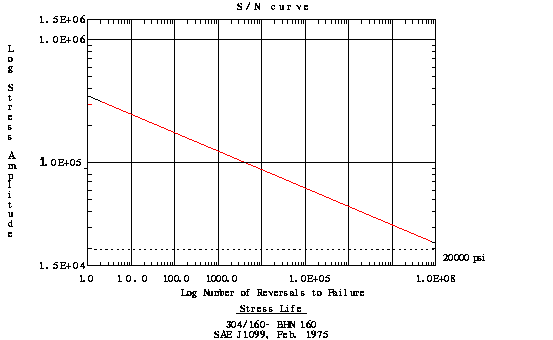
La ecuación es la siguiente:
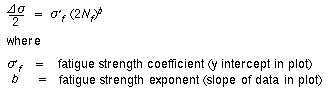
q Strain-Life
La ecuación de deformación unitaria-vida (strain-life) se basa en la ecuación de tensión-vida. Intenta determinar la deformación plástica. La parte plástica de la ecuación se puede escribir como:

Combinando las ecuaciones de tensión-vida con deformación unitaria-vida se obtiene lo siguiente:
![]()
El número de ciclos para el fallo, en cuyo punto se cruzan las ecuaciones elásticas y plásticas de deformación-vida, se llama vida a fatiga de transición.
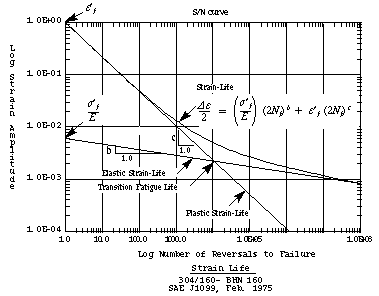
Estimación del Daño

Una vez calculado el número de ciclos para el fallo para cada rango (o amplitud), se pasa a calcular el daño.

El daño total se calcula sumando el daño causado por cada rango. El nº de sucesos (events) para el fallo (o el nº de veces que la historia de cargas o deformaciones puede repetirse hasta el fallo) es la inversa del daño total.
Tensiones Medias No Nulas (Mean
Stress)

Para predecir correctamente la vida a fatiga en estructuras precargadas o con componentes medias de la tensión no nulas hay que incluir la tensión media no nula en los cálculos ya que también colabora en el fallo a fatiga de la estructura. No es posible aplicar directamente ningún criterio basado en el principio de superposición de componentes alternas y medias de la tensión, hay que realizar ensayos sistemáticos sobre piezas y probetas con diferentes combinaciones de tensión llevando los resultados al conocido diagrama de Haigh como el de la siguiente figura:
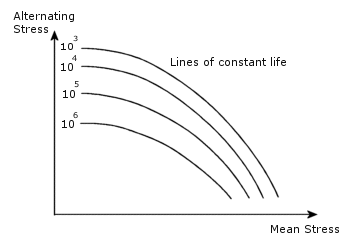
Esto se puede hacer de dos maneras:
Calcular una tensión equivalente para cada rango |
|
Incluir la tensión media no nula en las ecuaciones de vida a fatiga |
q Métodos de Tensiones Equivalentes
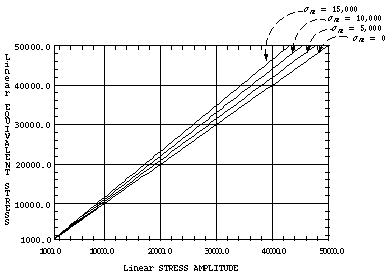
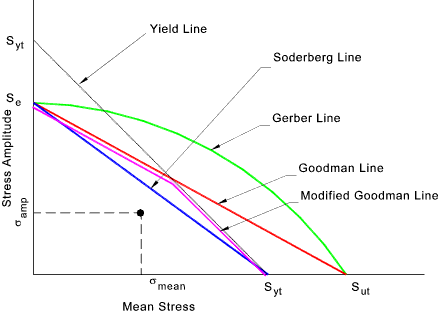
La amplitud de tensión utilizada en la ecuación de Tensión-Vida puede incluir tensiones medias no nulas usando un método de tensiones equivalentes. Esos métodos se basan en la utilización de la tensión variable (o amplitud de tensión) y tensión media para calcular un nuevo valor de la tensión llamado tensión equivalente que reemplaza al valor de la tensión variable en la ecuación de tensión-vida. Los principales criterios de tensión equivalente utilizados hoy en día son los de Gerber, Goodman, Soderberg y Morrow. El método de Goodman es adecuado para materiales frágiles, mientras que Gerber es en general más adecuado para materiales dúctiles, y por último Soderber es el más conservativo.
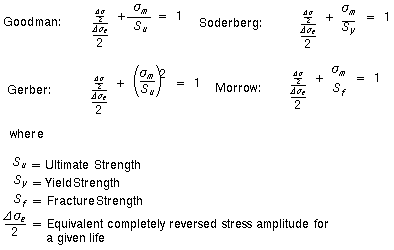
La siguiente imagen muestra una curva 360/160 usando el método de tensión equivalente de Goodman para líneas constantes de tensión media no nula:
q Tensiones Medias no nulas en las ecuaciones de Vida a Fatiga
Para utilizar las tensiones medias no nulas directamente en la ecuación de vida a fatiga, primero debe incluirse durante el conteo de ciclos.. Esto es un problema si se dispone de una historia de deformaciones unitarias en vez de tensiones. Es sencillo obtener la deformación media no nula tras el conteo de ciclos, pero las tensiones medias no nulas no están disponibles.
Conteo de Rainflow con Tensiones
Medias no nulas

Las deformaciones unitarias medias no se pueden convertir a tensiones medias directamente mediante la ecuación cíclica de tensión-deformación. Considerar el siguiente bucle de histéresis:
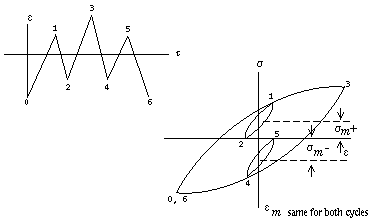
El pequeño bucle (4-5-4 y 1-2-1) incluido dentro del gran bucle (0-3-6) tiene los mismos rangos de deformación unitaria. Usando la ecuación cíclica de tensión-deformación unitaria, los rangos de deformación se pueden convertir a rangos de tensión iguales entre sí. Los rangos de deformación media para ambos bucles son iguales. Sin embargo, la tensión media es diferente para los dos bucles, ya que una es positiva y la otra es negativa.
Hace falta un método que permita obtener tensiones medias no nulas a partir de una señal de entrada basada en deformaciones unitarias.
Esto se puede conseguir de forma bastante eficiente partiendo el bucle de histéris grande en elementos discretos. En vez de realizar conversiones de cada valor de la deformación para determinar el correspondiente valor de tensión, se puede construir una matriz de valores de deformación con su correspondiente valor de tensión en función del tiempo. Cuantos más elementos se usen mejor es la aproximación del bucle de histéresis.
Una vez localizados los rangos de deformación o tensión y las correspondientes tensiones medias, se puede pasar a estimar la vida a fatiga. las ecuaciones de tensión-vida y deformación-vida se pueden modificar para incluir los efectos de tensiones medias no nulas.
q Stress-Life
La ecuación de tensión-vida se puede modificar para incluir los efectos de tensiones medias restando las tensiones medias del coeficiente de resistencia a la fatiga:
![]()
q Strain-Life
Las tensiones medias se pueden incluir en la ecuación de deformación-vida haciendo lo mismo que en la curva de tensión-vida:
![]()
q Smith, Topper y Watson
Smith, Topper, y Watson desarrollaron otro método para incluir los efectos de tensión media en la ecuación de deformación-vida:
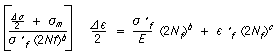
Esta ecuación también se puede escribir como:
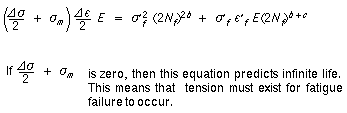
Daño Acumulado

Existen dos métodos:
Primero se cuentan todos los ciclos y seguidamente se estima el daño |
|
El conteo de ciclos y la estimación de daño se realiza simultáneamente. |
El primer método consiste en crear un histograma de rangos de ciclos contados y seguidamente meter los rangos de ciclos en las ecuaciones de vida a fatiga. La precisión de la estimación de daño depende de la resolución del histograma -- a mayor resolución mayor precisión.
Usando el segundo método se obtienen mejores estimaciones del daño porque el daño se estima para cada ciclo según se encuentra. En este caso no se depende de la resolución utilizada y también permite considerar el efecto de la secuencia de cargas.
Resultados del Análisis de Fatiga

Durante el análisis, los parámetros de variación de la carga se combinan con otros criterios de fatiga y el programa realiza los cálculos de fatiga para evaluar la durabilidad de la estructura cuyos resultados se representan mediante contornos en color en las siguientes áreas:
Resistencia Estructural (Factor de Seguridad a Tensión -- SSF: Stress Safety Factor) |
|
Resistencia a Fatiga (Factor de Seguridad a Fatiga -- FSF: Fatigue Safety Factor) |
|
Vida a Fatiga |
|
Factor de Daño |
q Factor de Seguridad a Tensión:
El factor de seguridad a tensión (SSF) es
una media de la resistencia global de la estructura y se evalúa dividiendo el criterio de
tensión (por ejemplo, el límite elástico del material) por la tensión efectiva (por
ejemplo, vonMises, Tresca o la tensión principal máxima/mínima). El programa calcula el
SSF como una función de la historia de la tensión efectiva (vonMises, Tresca o max/min
de la tensión principal) para determinar el factor de fallo de la estructura. Los valores
por encima de 1.0 son aceptable, mientras que valores por debajo de 1.0 indican fallo. Si
el SSF es menor de 1.0 no es necesario realizar ningún análisis de fatiga ya que la
estructura ha plastificado por tanto un rediseño es necesario.
q Factor de Seguridad a Fatiga:
El factor de seguridad a fatiga (FSF)
predice si la estructura fallará debido a cargas cíclicas. El FSF se calcula primero
identificando todos los ciclos de carga (tensiones medias y tensiones variables) y
seguidamente mediante el Diagrama de Goodman se obtienen los ciclos más desfavorables. El
criterio de Goodman proporciona una estimación más conservadora del FSF, lo que
significa que utilizando Goodman se tiende a sobredimensionar el diseño.
El criterio de Goodman utiliza dos propiedades del material:
la tensión última, su |
|
y la máxima tensión alterna (o variable), samp |
Un ejemplo del criterio de Goodman se tiene en la siguiente figura donde el eje-X es la tensión media y el eje-Y es la tensión variable (o alterna, o amplitud de tensión).
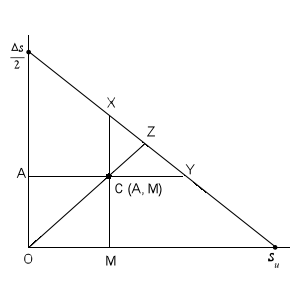
En el ejemplo anterior el pto. C es la tensión en un ciclo, donde A es la tensión alterna del ciclo, M es la tensión media del ciclo y su es la tensión última del material. El valor Ds/2 es la máxima tensión alterna que no causa ningún daño en el material y por tanto el FSF = OZ/OC, cuando tanto la tensión media como la alterna son variables. Para que un diseño resulte seguro el FSF debe ser nayor que 1.0.
q Vida a Fatiga:
El resultado de vida a fatiga evalúa la
vida de la estructura calculando la inversa del daño. Usando la regla de Palmgren-Miner,
también conocida como la regla del daño lineal, el daño para cada ciclo de tensión o
deformación se combina para calcular el daño acumulado para todos los ciclos de carga de
servicio. La inversa del daño total es el nº de ciclos de carga de servicio antes de que
se inicia ninguna grieta o fallo en la estructura, con lo cual este valor puede usarse
para determinar la vida de la estructura.
Los criterios de vida a fatiga son los siguientes:
Smith-Watson-Topper |
|
Deformación-Vida (tensión principal máxima) |
|
Deformación-Vida (tensión cortante máxima) |
|
Tensión-Vida |
Cada criterio de vida define una curva S-N diferente basándose en el uso de ciertas propiedades del material a fatiga. Seeguidamente usando el conteo de ciclos Rainflow, el programa identifica la amplitud de tensión o deformación (o rango de tensiones o deformaciones) así como la tensión o deformación media de cada ciclo de la historia de carga de servicio. El daño de cada ciclo se calcula y se suma usando la curva S-N según el criterio de vida seleccionado.
Recomendaciones Prácticas de
Diseño a Fatiga

La mejor práctica de diseño en ingeniería es tratar de reducir al máximo el riesgo de fallos por fatiga en el diseño de piezas sometidas a cargas cíclicas. Se recomienda:
- Reducir/eliminar cargas cíclicas.
- Reducir operaciones - usar velocidades de rotación más bajas, reemplazar piezas de forma regular.
- Seleccionar materiales tolerantes a cargas cíclicas.
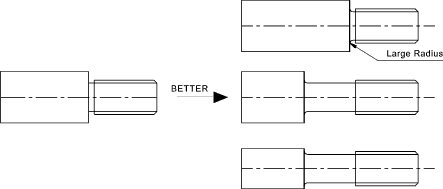
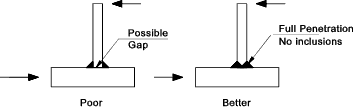
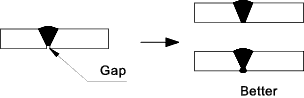
- Reducir/eliminar concentraciones de tensiones severas -- no permitir esquinas vivas o cambios de sección bruscos.
- Especificar procesos de fabricación que den resistencia a la fatiga -- trabajo en frío, granallado.
- Especifican tratamientos térmicos que aumenten la resistencia a fatiga -- Nitridación/Carburización.
- Sobredimensionar las piezas para reducir niveles de tensión.
- Precargar las piezas para convertir cargas cíclicas en cargas permanentes (precarga de tornillos).
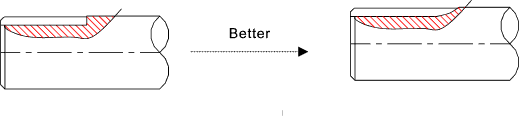
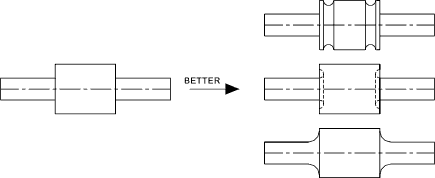
las siguientes figuras ilustran diferentes métodos para reducir concentración de tensiones:
Referencias

Rafael Avilés; "Análisis de Fatiga en Máquinas"; Thomson, 2005. |
|
H.O. Fuchs; R.I. Stephens; "Metal Fatigue in Engineering"; Wiley, 1980. |
|
D. Socie; "Fatigue-Life Prediction Using Local Stress-Strain Concepts''; Experimental Mechanics, February, 1977. |
|
D.F. Socie, M.R. Mitchell, and E.M. Caulfield; "Fundamentals Of Modern Fatigue Analysis"; College of Engineering, University of Illinois, April, 1977. |
|
Fatigue Design Subcommittee of Division 4 of SAE Iron and Steel Technical Committee; Fatigue Design Handbook; Society of Automotive Engineers, Inc., 1968. |
