FEMAP V10.1 & NX Nastran 6.1 Tutorial
NAFEMS Benchmark Composite Test R0031/3
(Septiembre, 2009)
1.
Introducción a los Materiales Compuestos Laminares (Composites)
El término "Composite" se refiere
a un material de ingeniería que está formado por más de un compuesto o
material. Para la Teoría Clásica de Láminas el término Composite se aplica a
un material que está compuesto de montones de capas plegadas o láminas, en
donde cada lámina tiene sus respectivas propiedades ortotrópicas. Un laminado
es un apilado de láminas individuales en donde cada lámina está orientada de
forma diferente a la direcciones del material principal. El laminado está todo
unido mediante una fina capa de material adhesivo que se considera que tiene
espesor cero. En FEMAP V9.3
(Abril 2007) se introdujeron capacidades avanzadas para trabajar con
materiales compuestos.
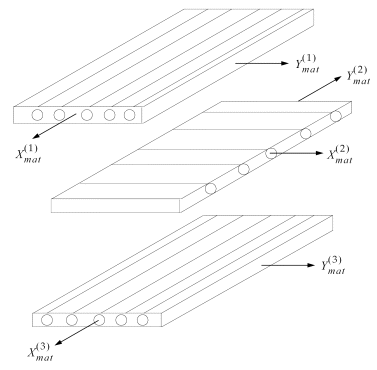
Láminas ordenadas formando un Composite
Cada capa o lámina puede considerarse como un grupo de fibras unidireccionales. La posibilidad de orientar las fibras en una dirección particular permite ajustar a medida las propiedades mecánicas un material compuesto laminar para soportar las cargas del entorno. Los ejes principales del material de la lámina son paralelos y perpendiculares a la dirección de las fibras. Las direcciones principales se denominan como:
-
“Longitudinal” o dirección-1 de la fibra
-
“Transversal” o dirección- 2 de la fibra para la dirección perpendicular (dirección de la matriz)
La siguiente figura muestra una vista explosionada de tres placas laminadas con capas cruzadas ("cross-ply"). La lámina-n (n = 1,2,3,4) de cada una de las tres configuraciones son normales al eje-Z del sistema de coordenadas indicado y los ejes 1 y 2 unidos a cada lámina individual denotan las direcciones de los ejes principales del material. Las direcciones de los ejes principales del material de cada lámina se alternan tal como indica la palabra "cross-ply" para describir la configuración. El plano X-Y del sistema de coordenadas está definido en el plano medio geométrico del laminado.
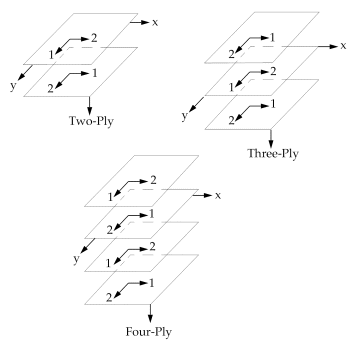
Vista explosionada de tres placas
laminadas con capas en cruz ("cross-ply")
Las capas están hechas en general de fibras pegadas sobre una matriz. Si la capa es una cinta, todas las fibras están orientadas en la misma dirección. Las capas de tejido tienen fibras en dos direcciones. Se pueden utilizar numerosos materiales tanto para fibras como matrices. Como ejemplos de fibras más comunes tenemos las fibras de carbono, vidrio, boro, carburo de silicio y tungsteno. Como ejemplos de matrices tenemos la resina epóxica y el aluminio.
Los materiales compuestos estructurales están formados tanto por composites como por materiales sencillos y sus propiedades dependen fundamentalmente de la geometría y de su diseño. Los más abundantes son los laminares y los llamados paneles sandwich:
-
Los laminares están formadas por paneles unidos entre si por algún tipo de adhesivo u otra unión. Lo más usual es que cada lámina esté reforzada con fibras y tenga una dirección preferente, más resistente a los esfuerzos. De esta manera obtenemos un material isótropo, uniendo varias capas marcadamente anisótropas. Es el caso, por ejemplo, de la madera contrachapada, en la que las direcciones de máxima resistencia forman entre sí ángulos rectos.
-
Los paneles sandwich consisten en dos láminas exteriores de elevada dureza y resistencia (normalmente plásticos reforzados, aluminio o incluso titanio) separadas por un material menos denso y menos resistente (polímeros espumosos, cauchos sintéticos, madera balsa o cementos inorgánicos). Estos materiales se utilizan con frecuencia en construcción, en la industria aeronáutica y en la fabricación de condensadores eléctricos multicapas.
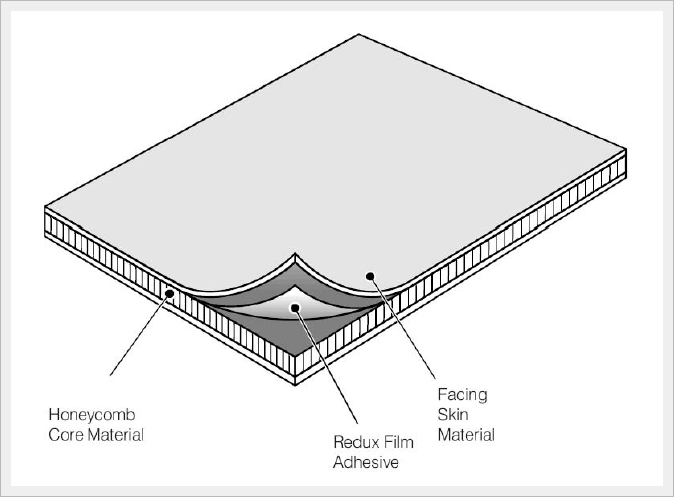
Composite tipo Sandwich
2.
Descripción del Problema
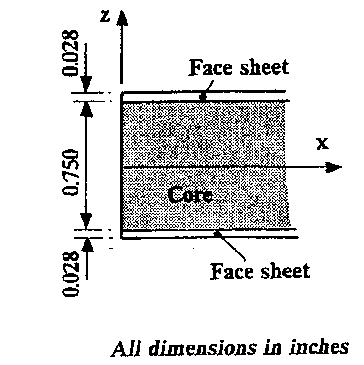
Se trata de estudiar el
comportamiento estructural de un composite tipo sandwich con núcleo tipo panal
de abeja (Honeycomb Panel) de dimensiones 10 x 10
pulgadas sometido a una presión normal uniforme de 100 psi. El Composite está
simplemente apoyado en las cuatro aristas. Por existir simetría de cargas y de
geometría se estudiará 1/4 del problema. El espesor de las láminas exteriores
(Face Sheet) es de 0.028 pulgas y el espesor del núcleo central (Core) es de
0.750 pulgadas.
Se pide obtener los siguientes resultados:
-
Tensiones SIGMA-XX y SIGMA-YY así como el desplazamiento máximo en el punto medio "C" de la placa (X=5,Y=5).
-
Tensión de cortadura TAU-XY en el punto "E" situado en el centro del primer cuadrante (X=2.5,Y=2.5).
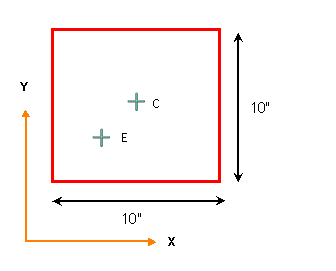
El modelo de Elementos Finitos se creará en FEMAP V10.1 y los resultados de desplazamientos y tensiones se calcularán con el solver NX NASTRAN 6.1.
3.
Definición de la Geometría en FEMAP
Directamente desde "Geometry > Surface > Corner"
definir
una superficie por cuatro puntos (0,0,0), (5,0,0), (5,5,0) y (0,5,0) que es
justamente 1/4 de modelo:
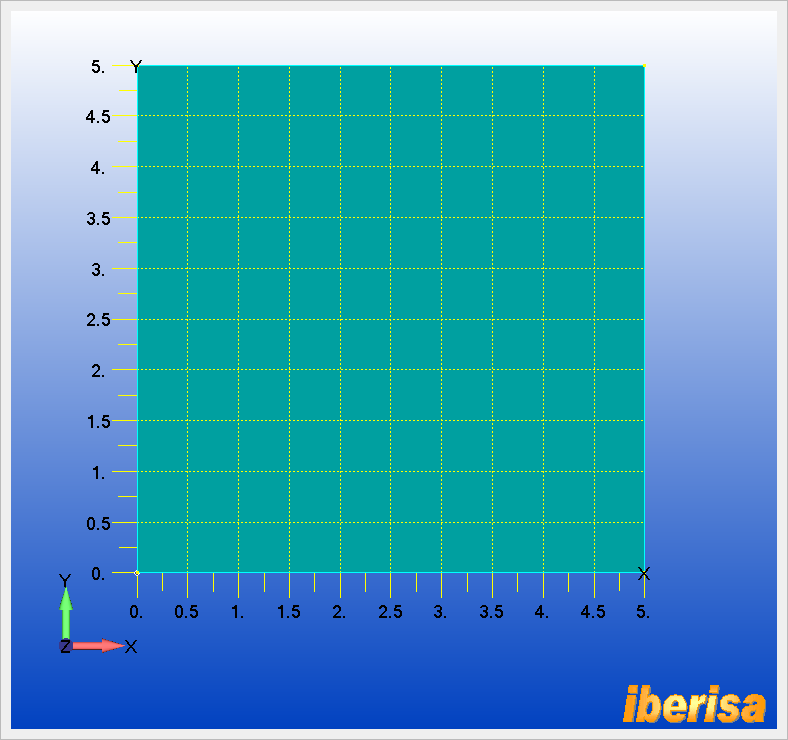
1/4 de placa de 5x5 pulgadas creada
en FEMAP
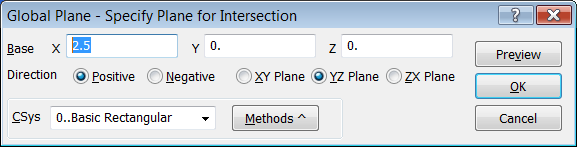
Para tener el Punto "E" lo más sencillo es dividir la superficie en cuatro partes iguales con la orden "Geometry > Solid > Split", seleccionamos el método "Global Plane", partimos por el plano YZ por el punto (2.5,0,0) y repetimos la orden cortando las dos superficies por el plano ZX por el punto (0,2.5,0), resultando en 4 nuevas superficies:
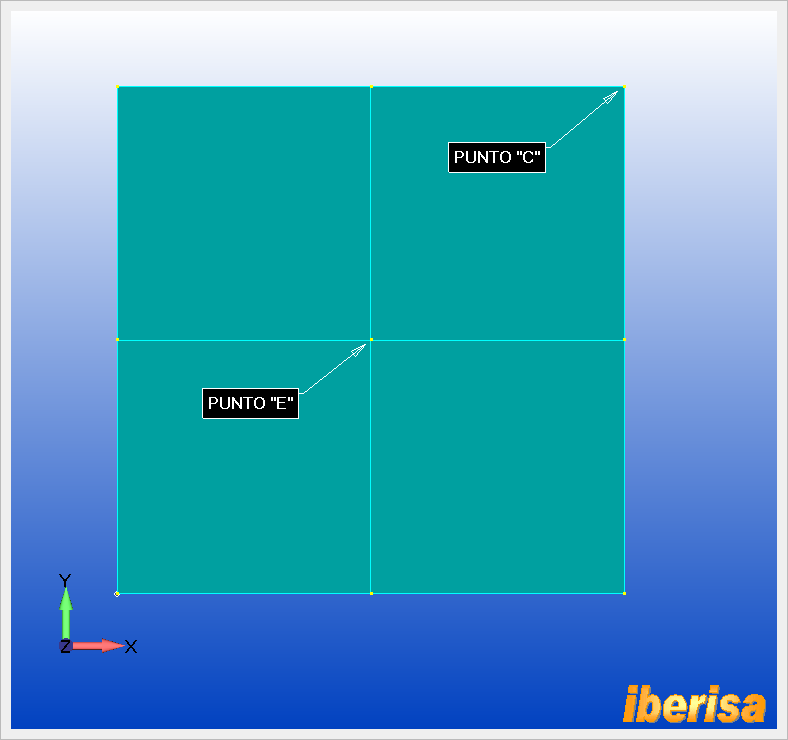
1/4 de placa dividida en cuatro
partes
4.
Definición de las Propiedades Ortotrópicas del Material
Desde "Model > Material" definimos las
propiedades de material para las láminas exteriores y el núcleo. Haz click en
el botón TYPE y selecciona el tipo de material "ORTHOTROPIC (2D)",
escribe un nombre para el material (por ejemplo "Face Sheet") y mete
las siguientes propiedades:
| Propiedad | Valor |
|---|---|
| Mass density | 1E-4 lbf-sec2/in4 |
| Young’s modulus X (E1) | 1E7 psi |
| Young’s modulus Y (E2) | 4E6 psi |
| Poisson’s ratio X (nu12) | 0.3 |
| Shear modulus X (G12) | 1.875E6 psi |
| Shear modulus Y (G13) | 1.875E6 psi |
| Shear modulus Z (G23) | 1.875E6 psi |
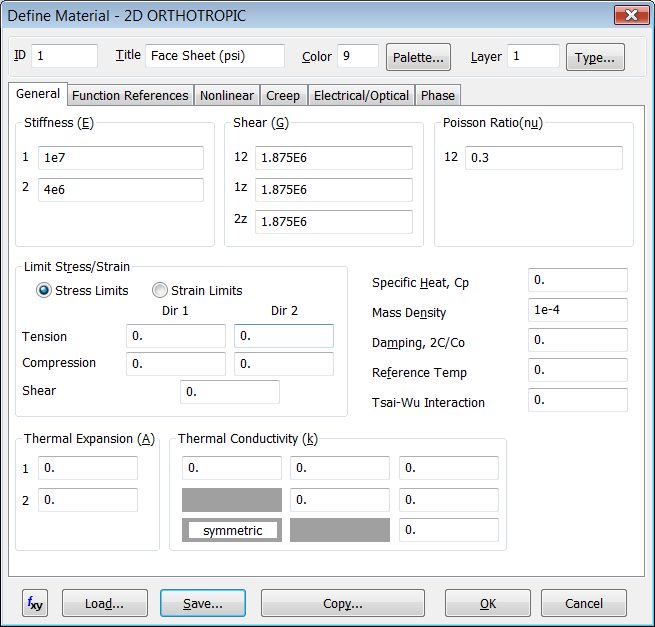
Material Ortotrópico nº 1
correspondiente a la lámina exterior
De igual forma metemos las siguientes propiedades del núcleo que como podemos ver por las propiedades apenas tiene rigidez:
| Propiedad | Valor |
|---|---|
| Mass density | 1E-4 lbf-sec2/in4 |
| Young’s modulus X (E1) | 10 psi |
| Young’s modulus Y (E2) | 10 psi |
| Poisson’s ratio X (nu12) | 0. |
| Shear modulus X (G12) | 10 psi |
| Shear modulus Y (G13) | 3E4 psi |
| Shear modulus Z (G23) | 1.2E4 psi |
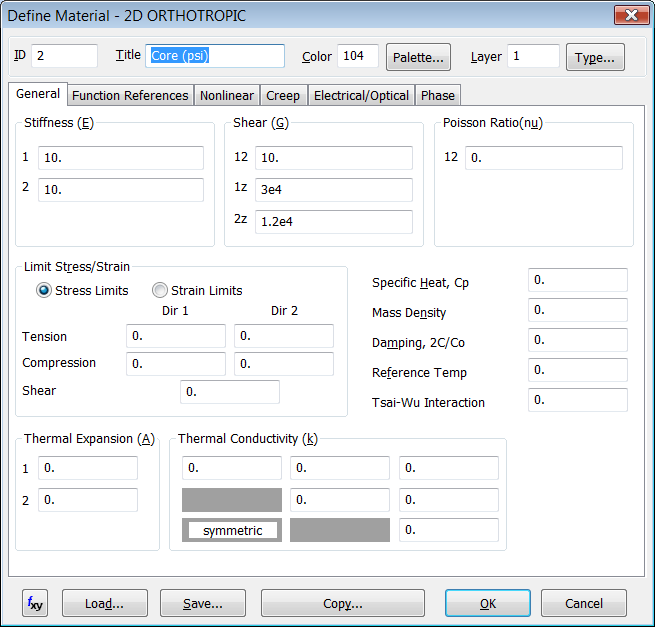
Material Ortotrópico nº 2
correspondiente al núcleo
La sección "Limit Stress/Strain" se usa para calcular los índices de fallo. Hay varios índices que Nastran calcula:
-
Hill
-
Hoffman
-
Tsai-Wu, y
-
Maximum Strain
Tsai-Wu require meter un valor experimental función del material, y es en la definición del material donde se debe especificar este valor. En este caso no se nos facilitan los valores límite de tensión a tracción, compresión y cortadura así que no calcularemos ningún índice de fallo.
5.
Definición del Layout del Composite
Tras definir las propiedades ortotrópicas de los diferentes
materiales que forman el composite, pasamos a definir en FEMAP cómo se sitúan
las capas laminadas mediante el Layout Editor desde "Model >
Layout". Aquí tenemos la clásica configuración llamada "honeycom
panel" en la que las capas superior e inferior son de un material muy
rígido mientras que el núcleo está formado por un material de bajo peso. En
el campo "Material" seleccionar el material 1 correspondiente a una de
las láminas exteriores, asignar un espesor de 0.028 pulgadas y un ángulo de 0
grados: esto significa que la dirección del material 1 de la lámina exterior
está alineado con el eje-X del sistema de coordenadas absoluto. Haz click sobre
"New Ply":
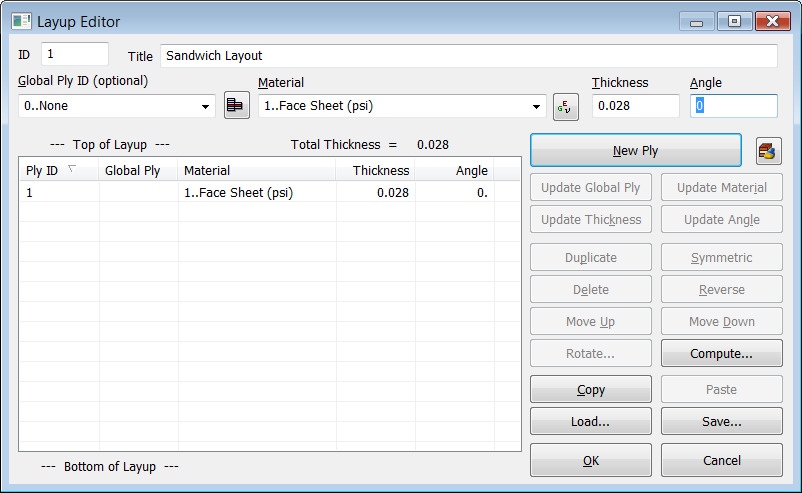
Definición de la capa
Seguidamente definimos la capa nº2 correspondiente al núcleo del composite: en el campo "Material" seleccionar el material 2 correspondiente al núcleo, asignar un espesor de 0.75 pulgadas y un ángulo de 0 grados: esto significa que la dirección de la cinta del núcleo está alineado con el eje-X del sistema de coordenadas absoluto. Haz click sobre "New Ply":
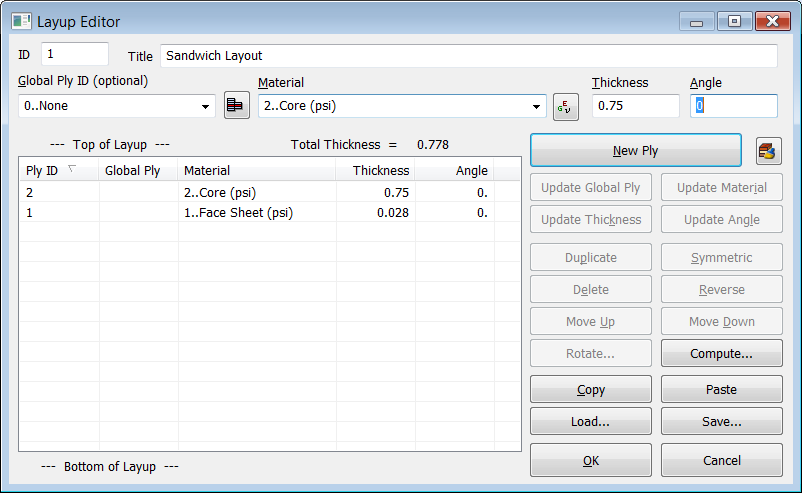
Definición de la capa
Para definir la capa nº3 correspondiente a la lámina exterior por ejemplo selecciona la capa nº 1 y haz click en el botón "Copy" y seguidamente en "Paste", y tendremos creado el Layout final del Sandwich de espesor total = 0.806 pulgadas:
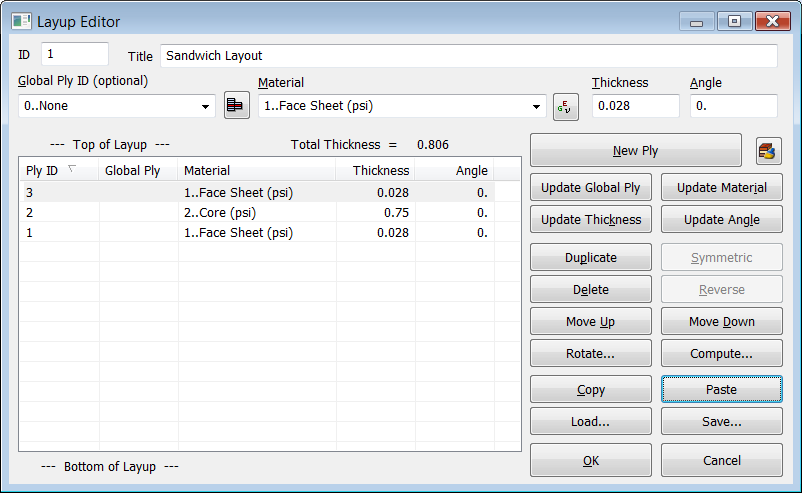
Definición de la capa
A la derecha del botón "New Play" tienes un icono que permite pre-visualizar el Layout, obteniendo la siguiente imagen:
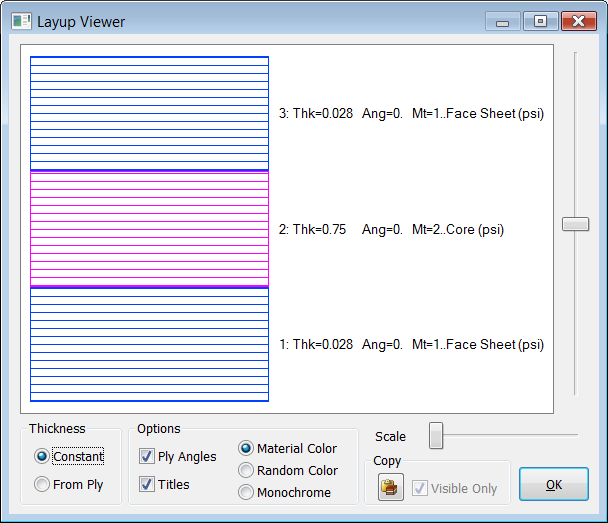
Previsualización del Layout del
Composite
El Layout de FEMAP ofrece una gran opción para obtener las propiedades isotrópicas equivalentes del composite. Pulsando sobre el botón "Compute" FEMAP calcula las propiedades completas del composite y las muestra en la ventana de mensajes, así como en la ventana "Entity Info":
| Laminate
Equivalent Properties 3 Plies - Total Thickness = 0.806 In-Plane Properties Bending/Flexural Properties A Matrix B Matrix D Matrix A-Inv Matrix B-Inv Matrix D-Inv Matrix |
6.
Definición de las Propiedades Laminate
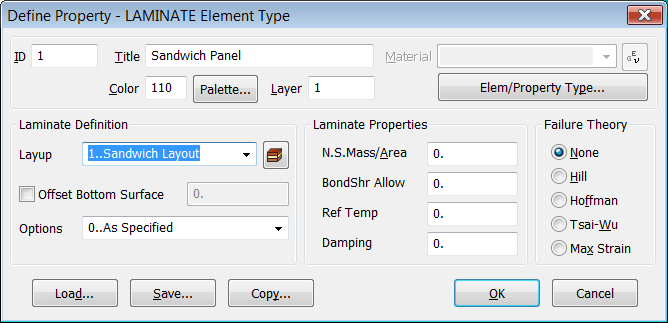
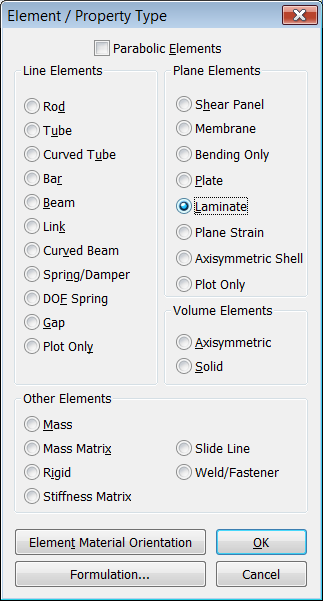
Dentro de las propiedades del tipo de elemento Laminate podemos definir el parámetro
"BondShr Allow" que permite calcular el factor de seguridad de la
unión (este valor se obtiene dividiendo la tensión cortante entre capas por el
parámetro "BondShr Allow"). También aquí se especifica la Teoría de Fallo
deseada (Hill, Hoffman, Tsai-Wu o Max Strain). Estas teorías de fallo producen índices de fallo.
Así, un
índice mayor de 1 denota fallo. Cada capa del laminado tendrá un índice de
fallo asociado.
7.
Definición de la Densidad de Malla
Seguidamente asignamos la densidad de malla a todas las
superficies mediante "Mesh > Mesh Control > Size on Surface".
Mallaremos con un tamaño de elemento de 0.625 que corresponde a una malla de
8x8 elementos, es decir, Tamaño de Elemento = Long. Curva / Nº de Elementos =
5/8 = 0.625.
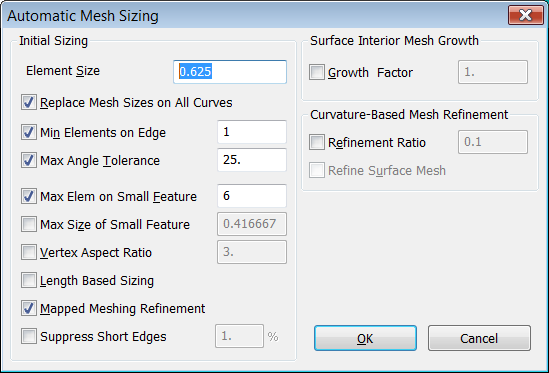
Definición del Tamaño del Elemento
En FEMAP podemos pre-visualizar el nº de divisiones en cada curva antes de mallar mediante "F6 > Labels, Entities, ..> Curve - Mesh Size > 3..Symbols & Count > Draw Entity ON". Nota: asegurarse que las curvas están visibles mediante "Ctrl-Q"
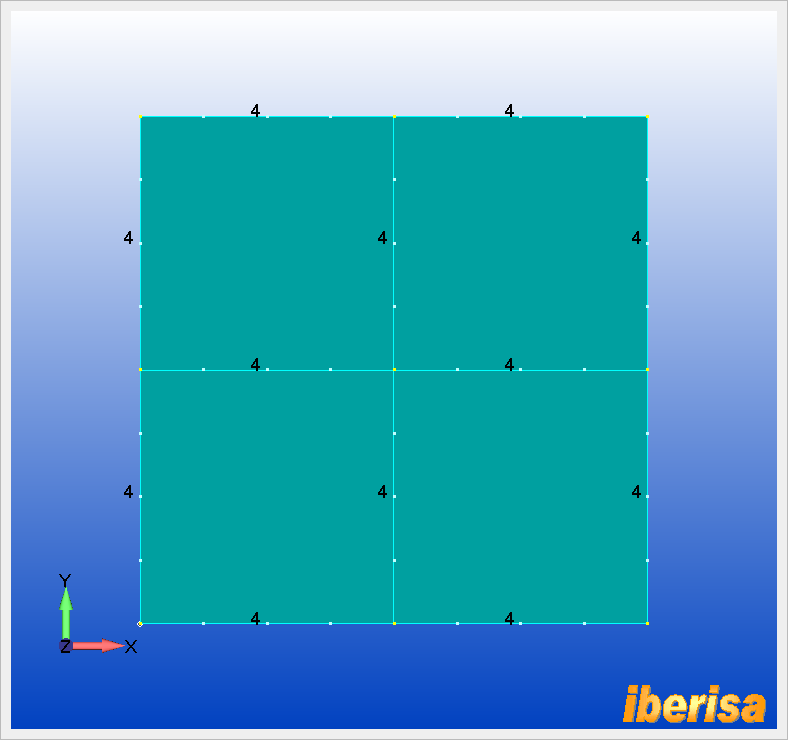
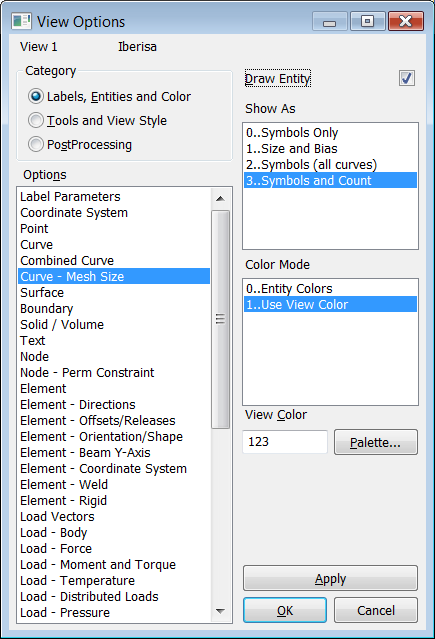
Previsualización del nº de
divisiones en las curvas del modelo
8.
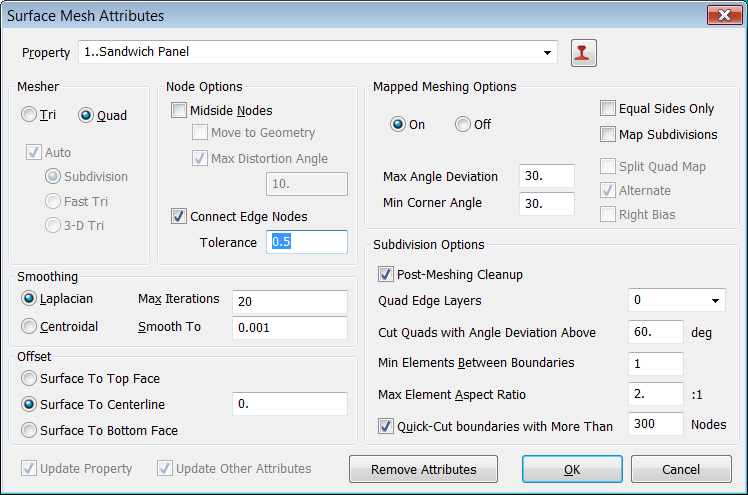
Asignación de Atributos a las Superficies
Antes de mallar las superficies asignamos la propiedad de
tipo de elemento y material directamente a la geometría mediante "Mesh >
Mesh Control > Attributes on Surfaces". En la opción "Connect
Edge Nodes" asegúrate de meter un valor de tolerancia razonable, por
ejemplo, 0.5, de esta forma se garantiza que FEMAP mergee nodos comunes entre superficies
con lados coincidentes:
9.
Mallado de Superficies
Mallamos todas las superficies mediante "Mesh >
Geometry > Surface". FEMAP automáticamente mergea nodos
coincidentes entre curvas de superficies. Con "Ctrl-Q" puedes ver los
nodos y elementos del modelo con sus etiquetas respectivas:
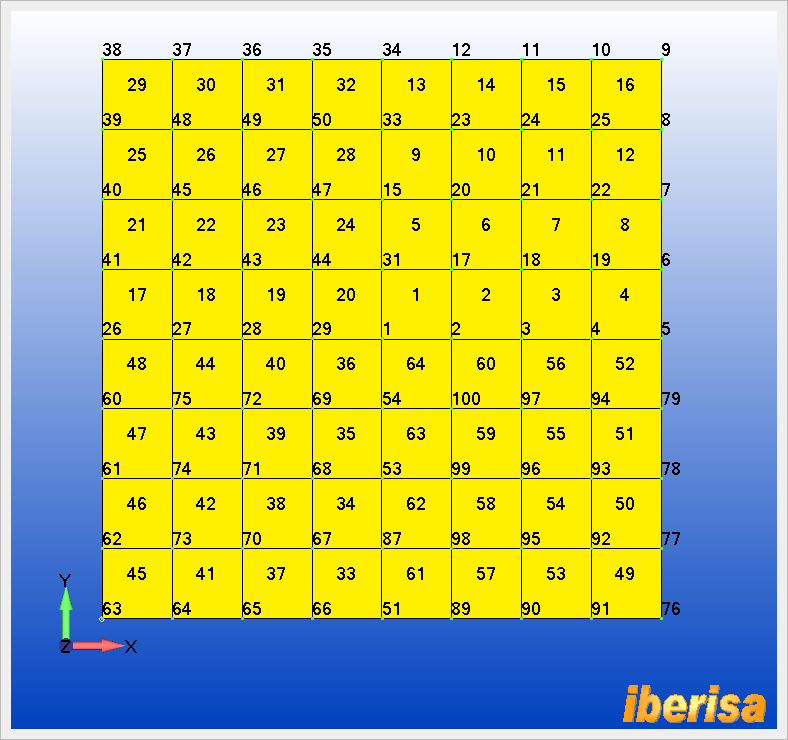
Aprovechando la visualización de
etiquetas de nodos y elementos vemos que el nodo#1 corresponde al Punto-E y el
nodo#9 al Punto-C,
el nodo#9 pertene al Elemento#16, y el nodo#1 está rodeado
por los elementos#1,20,36 y 64
10.
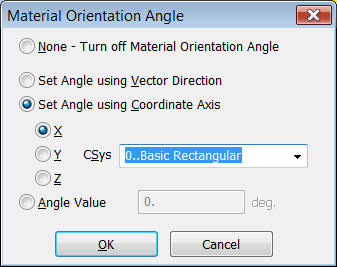
Especificar el Angulo del Material
Tras mallar el composite es necesario asignar a todos los
elementos un ángulo específico correspondiente a la dirección principal del
Layout mediante "Modify > Update Elements > Material Angle".
En este caso seleccionar el eje-X del sistema de coordenadas global cartesiano.
Es importante asegurarse que todos los elementos laminares tienen asignado un
ángulo. Nastran no ejecuta el análisis si los elementos no tienen asignado un
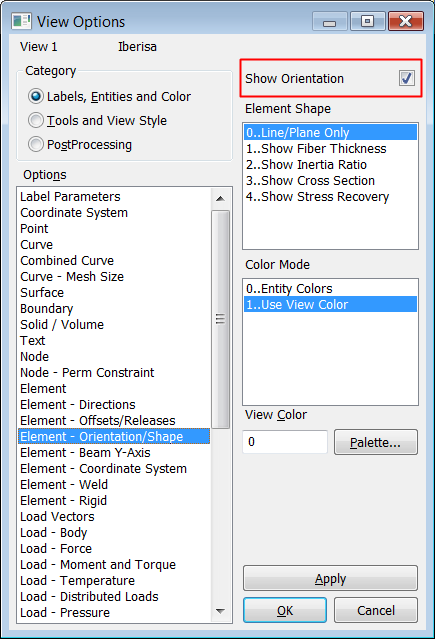
ángulo. Para visualizar el ángulo del material ir a "F6 > Labels, Entities, ..>
Element - Orientation/Shape > Show Orientation ON". También es
importante verificar las normales de los elementos mediante "F6 > Labels, Entities, ..>
Element - Directions > Show Direction ON":
11.
Aplicación de Condiciones de Contorno
La placa está simplemente apoyada en los cuatro bordes, y además debido
a la existencia de simetría de cargas y geometría estudiaremos 1/4 de modelo,
así que las condiciones de contorno a aplicar están resumidas en la siguiente
imagen:
Condiciones de Contorno
Las siguientes imágenes explican de forma secuencial el proceso a seguir para aplicar la condición de contorno en el borde izquierdo de la placa llamado "Apoyo Simple (TY=TZ=RX=0)" desde "Model > Constraint > Curve":
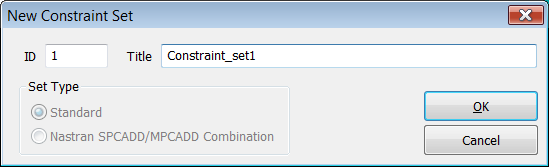
Definimos el set de restricción
nº1
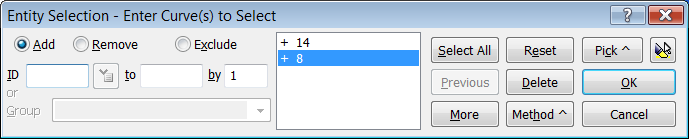
Selecionamos las curvas a aplicar la
restricción
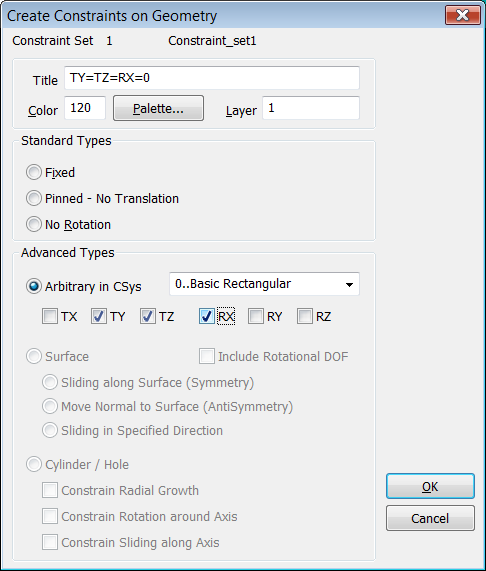
Definimos restricciones en el
sistema de coordenadas global cartesiano
Repitiendo el proceso de forma ordenada para el resto de curvas del modelo tendremos el siguiente resultado final:
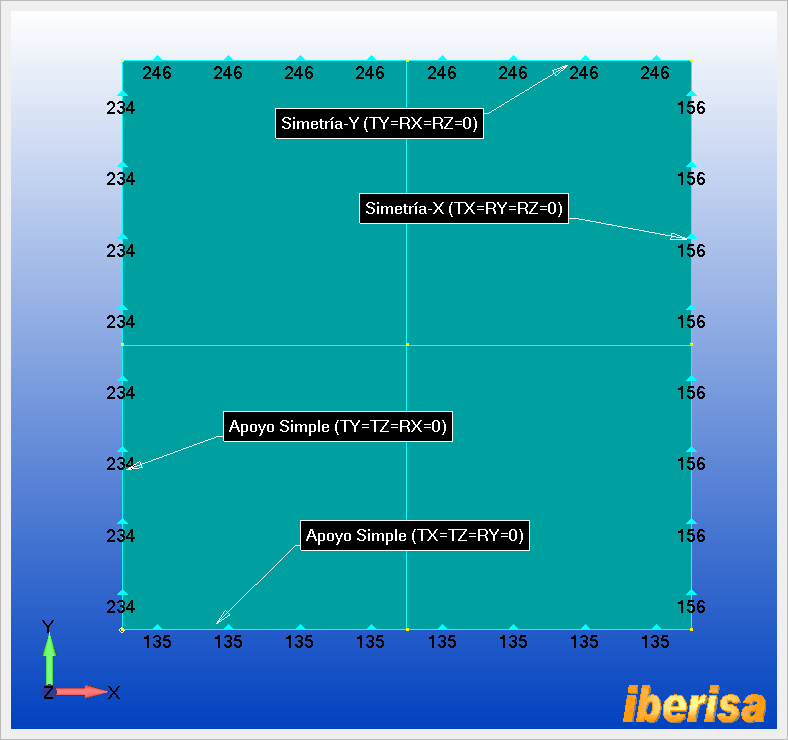
Resultado final con todas las
condiciones de contorno aplicadas
12.
Aplicación de Cargas
Desde "Model > Load > On Surface" aplicamos una presión
normal uniforme de valor 100 psi a todas las superficies del modelo:
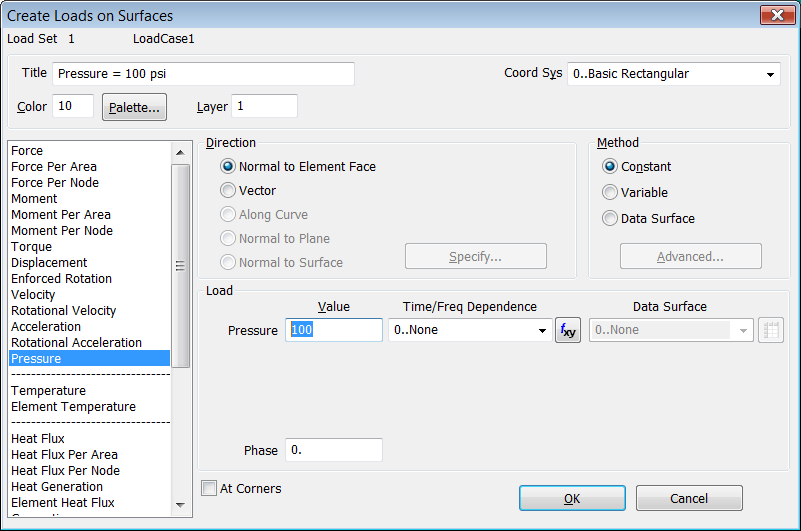
Presión normal y uniforme en todas
las superficies
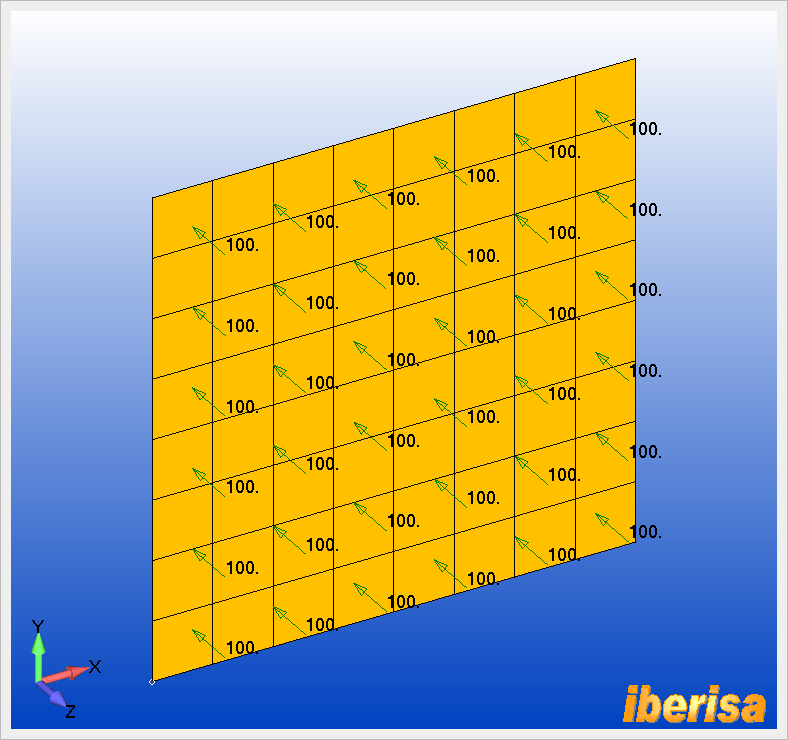
Resultado de la distribución de las
cargas de presión
13.
Definición del Tipo de Análisis
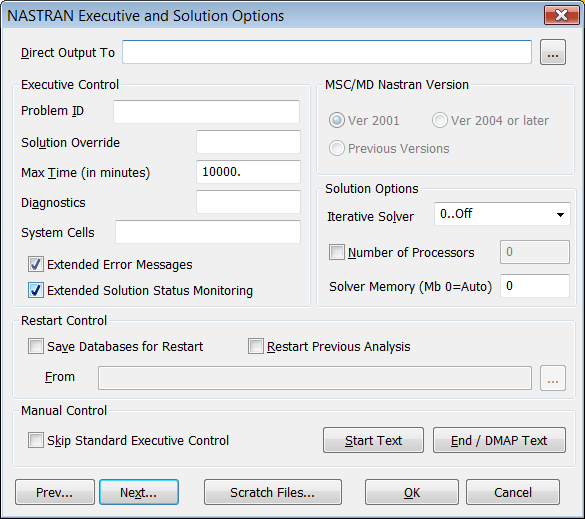
Desde "Model > Analysis" haz click en "New..."
para definir los parámetros del análisis estático lineal SOL101 con el solver
NX Nastran. Aceptamos todas las opciones por defecto y ejecutamos el análisis
haciendo click sobre el botón "Analyze":
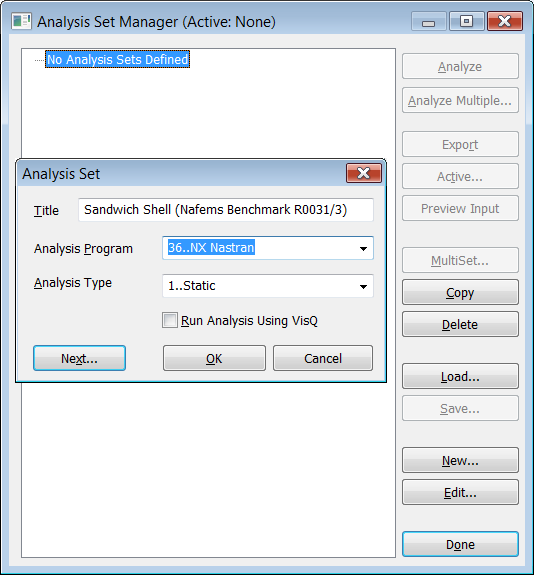
Defición del Análisis Estático
Lineal SOL101 con NX Nastran
../..
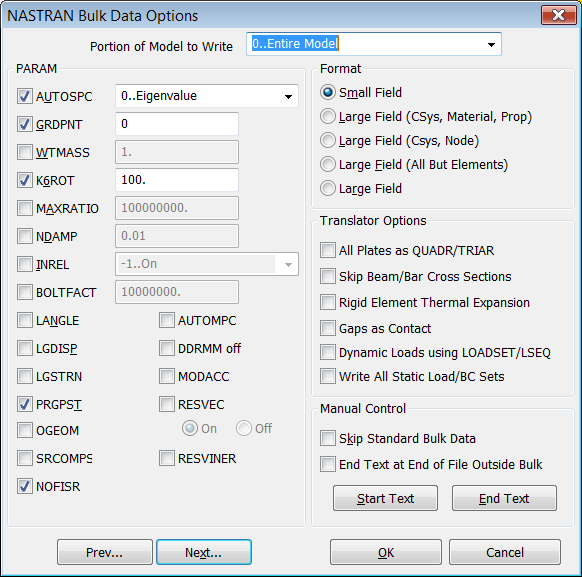
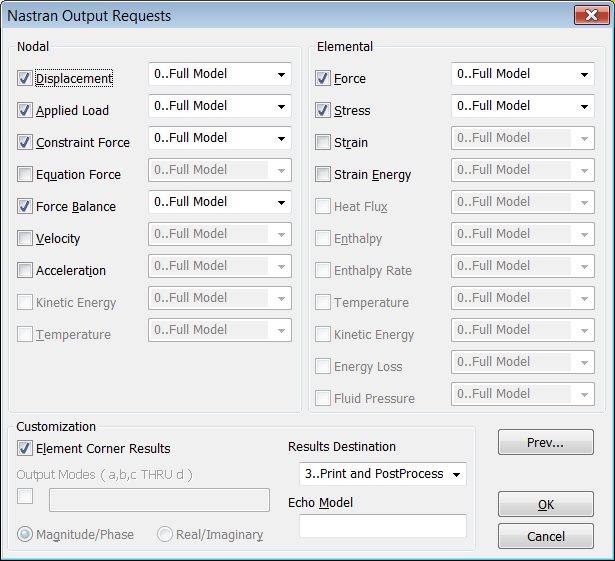
En la última pantalla seleccionado
"Results Dstination: 3..Print & Postprocesses"
tendremos un listado completo de resultados en el fichero *.F06
q
13.1.
Modelado de Composites en NX Nastran
NX Nastran usa elementos CQUAD4, CQUAD8, CTRIA3, y CTRIA6 para
modelar composites y materiales no uniformes. NX Nastran se basa en la teoría
clásica de láminas para la formulación del comportamiento de los elementos
Shell con propiedades de materiales compuestos laminares y no uniformes.
NX Nastran permite modelar un Composite con múltiples capas con un único elemento Shell con la opción PCOMP ya que las propiedades de material del compuesto laminar quedan reflejadas por completo en las matrices del módulo de elasticidad del elemento. El programa calcula automáticamente dichas matrices a partir de la definición del espesor, propiedades de material y orientación relativa de cada lámina. Una vez que el software calcule las matrices del módulo de elasticidad, se procede a ejecutar el análisis.
Debido a que las propiedades del material del compuesto laminar están completamente contenidas en las matrices del módulo de elasticidad, se puede usar un método estandard de obtención de resultados para calcular las tensiones en las láminas individuales así como las fuerzas que soporta cada lámina. Por tanto NX Nastran permite:
 |
Evaluar tensiones y deformaciones unitarias y aproximar índices de fallo en capas de forma individual. |
|
Calcular tensiones y deformaciones cortantes interlaminares así como índices de fallo. |
Si la carga en la estructura excede el límite elástico del material, entonces es necesario utilizar métodos no lineales para predecir la naturaleza del estado de deformación plástica (permanente). También es necesario realizar un análisis no lineal si el material presenta comportamiento no lineal en su rango elástico (modelo de material elástico no lineal).
En análisis 2-D de composites existen dos métodos para definir un laminado:
|
Método PSHELL: permite introducir directamente de forma explícita las relaciones constitutivas de rigidez de membrana, flexión, acoplamiento membrana-flexión y cortante. |
|
Método PCOMP: el composite se define de forma explícita, capa-a-capa. Cuanto se utiliza PCOMP, NX Nastran calcula las correspondientes entradas PSHELL y MAT2. |
En el análisis de composites 3D, el propio usuario debe introducir la matriz de material anisotrópica. Típicamente, se usa MAT9 para definir la matriz del material
q
13.2.
Método PCOMP
El método PCOMP es una forma eficiente de introducir
propiedades de materiales en composites a base de capas con fibras
unidireccionales. Las entradas de PCOMP consiste en la definición del material
capa-a-capa. Se puede usar PCOMP para definir el espesor, orientación, y el nº
de identificación del material de cada lámina individual.
Cuando se ejecuta el cálculo, NX Nastran calcula las propiedades del material del composite (membrana, flexión, cortante y acoplamiento flexión-membrana) como un todo a partir de los datos especificados en la entrada PCOMP. El programa saca las propiedades calculadas en la forma de una entrada PSHELL equivalente y cuatro entradas MAT2 equivalentes, tal como muestra la siguiente figura. Si se especifica ECHO = PUNCH en la sección "Case Control", el programa escribe las entradas PSHELL y MAT2 en un fichero PUNCH.
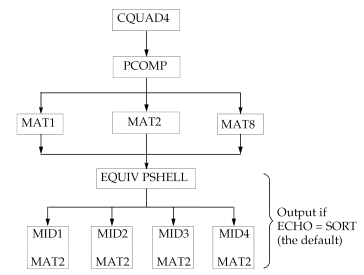
Generación de entradas PSHELL y
MAT2 equivalentes
INIT MASTER(S) NASTRAN SYSTEM(442)=-1, SYSTEM(319)=1 ID Model2,Femap SOL SESTATIC TIME 10000 CEND TITLE = Sandwich Shell (NAFEMS Benchmark R0031/3) ECHO = NONE DISPLACEMENT(PRINT) = ALL SPCFORCE(PRINT) = ALL OLOAD(PRINT) = ALL GPFORCE(PRINT) = ALL FORCE(PRINT,CORNER) = ALL STRESS(PRINT,CORNER) = ALL SPC = 1 LOAD = 1 BEGIN BULK $ *************************************************************************** $ Written by : Femap with NX Nastran $ Version : 10.10 $ Translator : NX Nastran $ Date : Mon Sep 14 12:42:26 2009 $ ********************************************************************* ../.. $ Femap with NX Nastran Property 1 : Sandwich Panel PCOMP 1 0. + + 1 .028 0. YES 2 .75 0. YES+ + 1 .028 0. YES $ Femap with NX Nastran Material 1 : Face Sheet (psi) MAT8 1 1.+74000000. .31875000.1875000.1875000. 1.-4+MT 1 +MT 1 0. 0. 0. +MA 1 +MA 1 $ Femap with NX Nastran Material 2 : Core (psi) MAT8 2 10. 10. 0. 10. 30000. 12000. 0.+MT 2 +MT 2 0. 0. 0. +MA 2 +MA 2 ../.. |
14.
Postprocesado de Resultados
La siguiente imagen muestra el aspecto que presenta el programa FEMAP with NX
Nastran una vez finalizado el cálculo. El máximo desplazamiento corresponde al
punto-C (nodo#9) y tiene un valor de 0.123 pulgadas que corresponde exactamente
con el valor objetivo de NAFEMS.
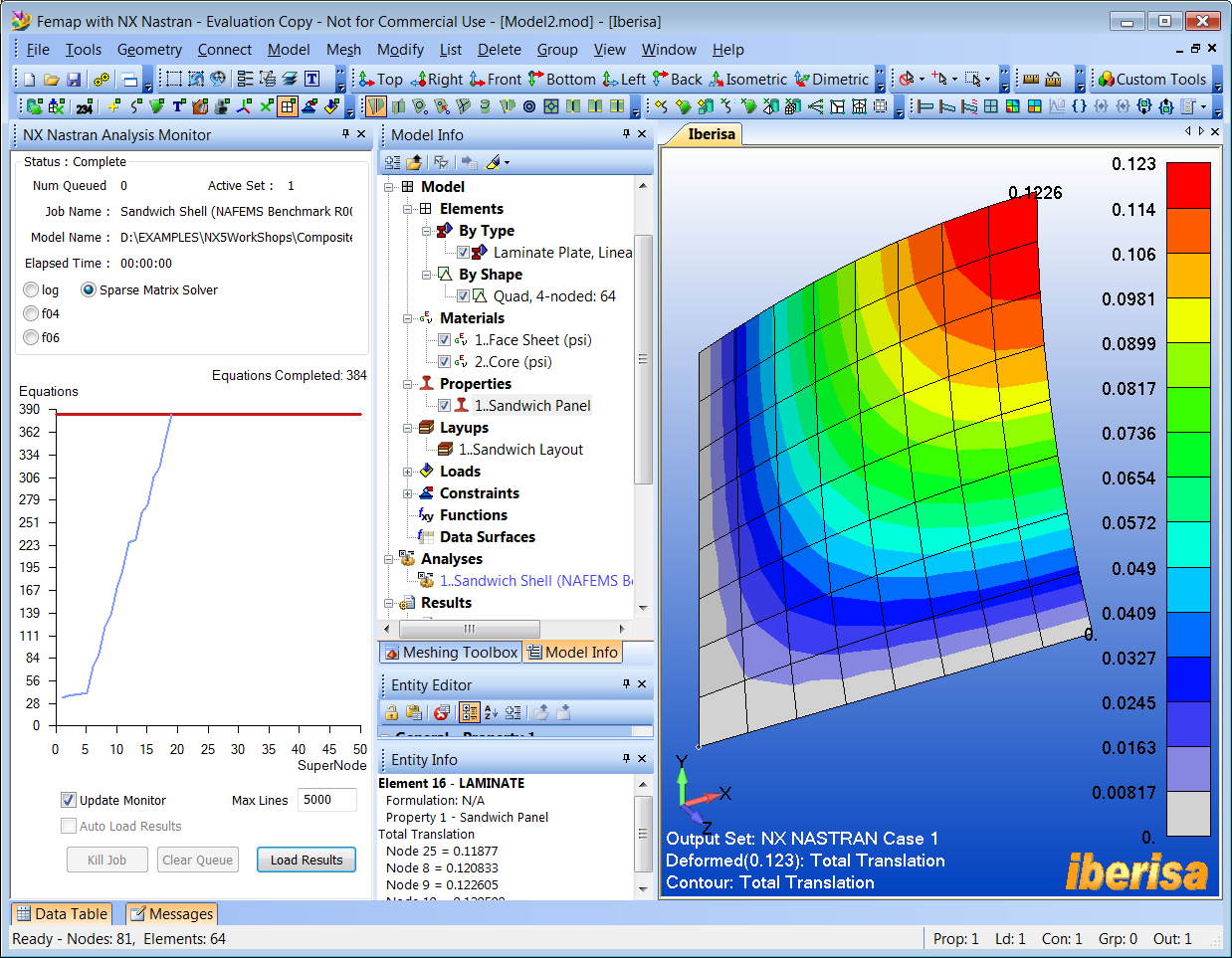
Resultados de Desplazamiento Máximo
en el Punto-"C"
Lo primero que me gusta comprobar siempre que realizo cualquier análisis es que las reacciones resultantes están en equilibrio con las cargas aplicadas. En efecto, la fuerza aplicada es 100 lb/in2x5inx5in=2500 lb, en perfecto acuerdo con la reacción obtenida RFZ=2.5e3 Lb.
* * * * * * * * * * * * * * * * * * * *
* * * * * * * * * * * * * * * * * * * *
* * * *
* * * *
* * * *
* * * *
* * N X N a s t r a n * *
* * * *
* * VERSION - 6.1 * *
* * * *
* * JAN 19, 2009 * *
* * * *
* * * *
* *Intel64 Family 6 Model 23 Steppi * *
* * * *
* *Intel(R) Core(TM)2 Quad CPU Q955 * *
* * * *
* * Windows Vista * *
* * * *
* * Compiled for X86-64 * *
* * * *
* * * * * * * * * * * * * * * * * * * *
* * * * * * * * * * * * * * * * * * * *
0
0 RESULTANTS ABOUT ORIGIN OF SUPERELEMENT BASIC COORDINATE SYSTEM IN SUPERELEMENT BASIC SYSTEM COORDINATES
0 SPCFORCE RESULTANT
SUBCASE/ LOAD
DAREA ID TYPE T1 T2 T3 R1 R2 R3
0 1 FX 0.000000E+00 ---- ---- ---- 0.000000E+00 0.000000E+00
FY ---- 0.000000E+00 ---- 0.000000E+00 ---- 0.000000E+00
FZ ---- ---- 2.500000E+03 4.519660E+03 -2.914388E+03 ----
MX ---- ---- ---- 1.730340E+03 ---- ----
MY ---- ---- ---- ---- -3.335612E+03 ----
MZ ---- ---- ---- ---- ---- 0.000000E+00
TOTALS 0.000000E+00 0.000000E+00 2.500000E+03 6.250000E+03 -6.250000E+03 0.000000E+00 |
Pulsar "F5 > Deform > Contour > Deformed & Contour Data > Lam Ply1 X Normal Stress" para representar las tensiones SIGMA-XX en la capa nº 1. Vemos que la máxima tensión se produce en el punto "C" (nodo#9, elemento#16) con un valor máximo de 34030 psi:
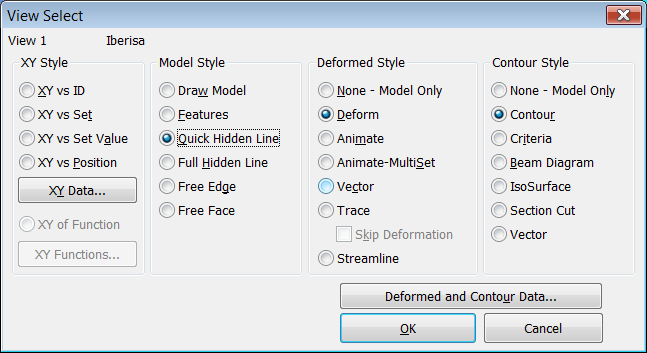
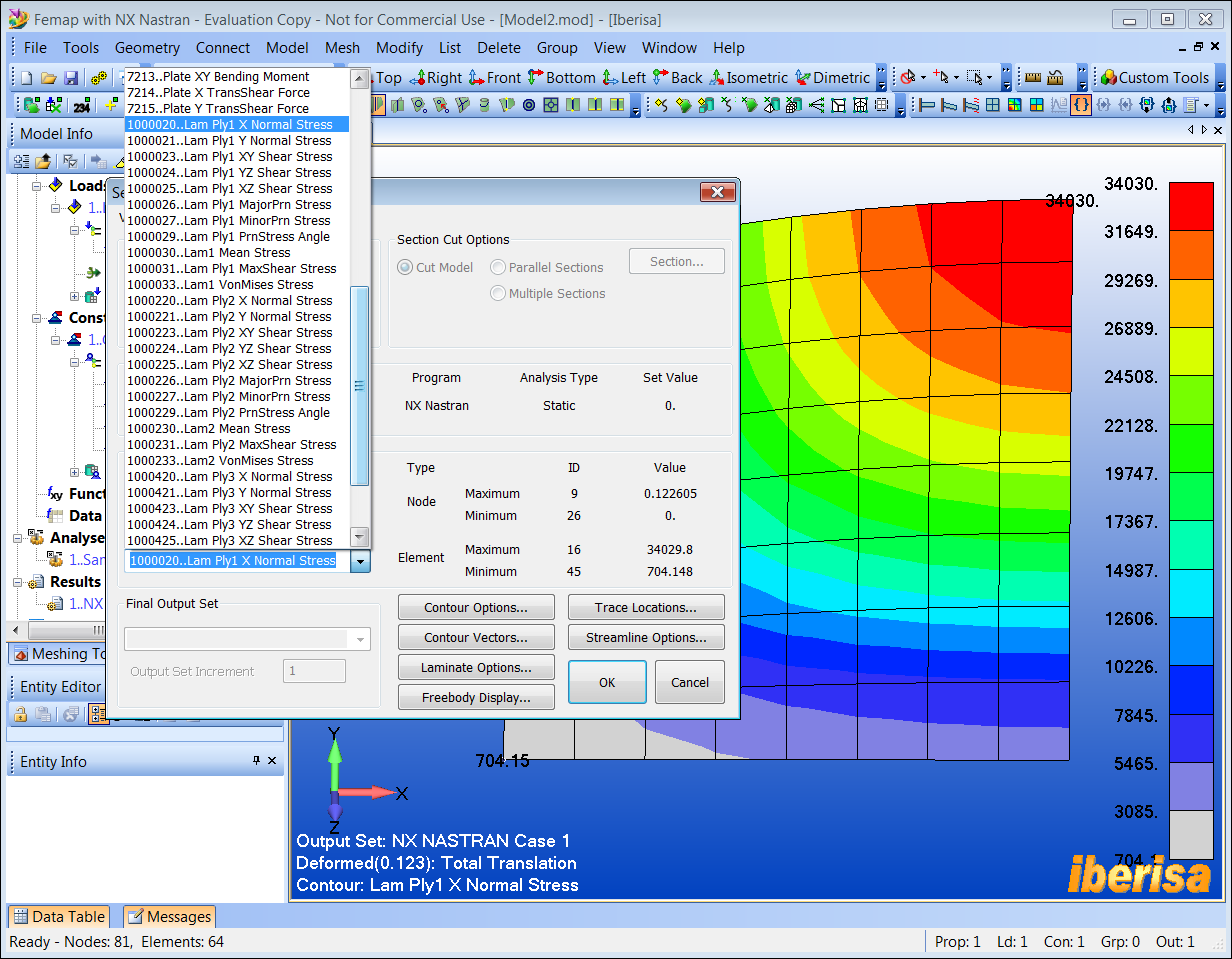
Resultados de Tensiones SIGMA-XX en
el Punto-"C"
Repetimos "F5 > Deform > Contour > Deformed & Contour Data > Lam Ply1 Y Normal Stress" para representar las tensiones SIGMA-YY en la capa nº 1. Vemos que la máxima tensión se produce en el punto "C" (nodo#9, elemento#16) con un valor de 13294 psi:
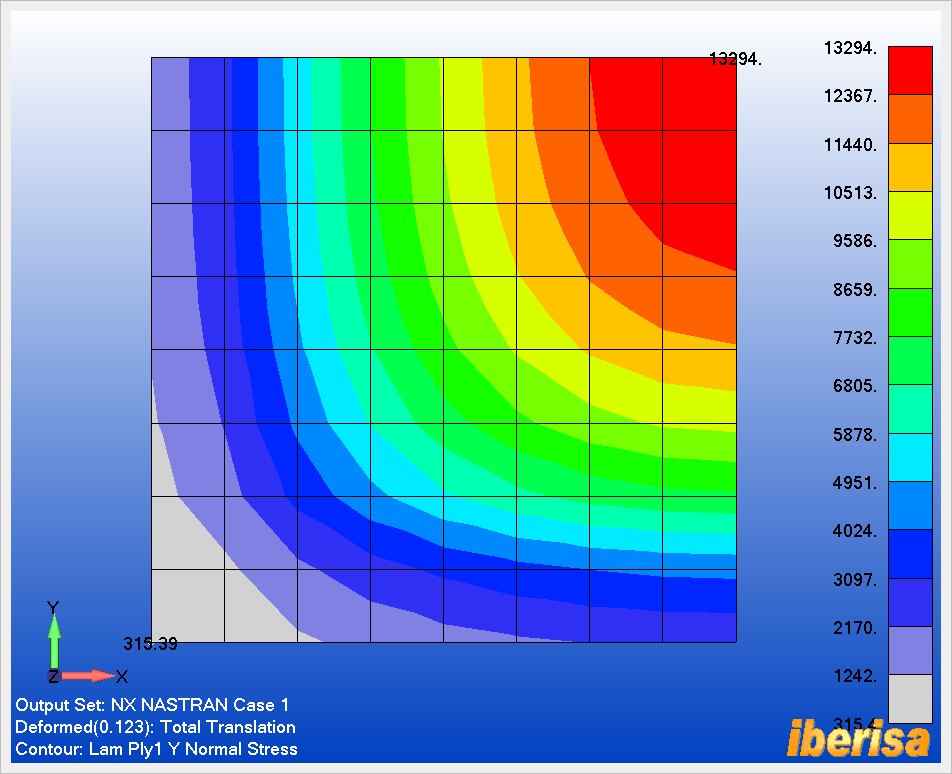
Resultados de Tensiones SIGMA-YY en
el Punto-"C"
Con elementos Laminares Composite NX Nastran calcula las tensiones sólo en el centro del elemento:
F O R C E S I N Q U A D R I L A T E R A L E L E M E N T S ( Q U A D 4 ) OPTION = BILIN
ELEMENT - MEMBRANE FORCES - - BENDING MOMENTS - - TRANSVERSE SHEAR FORCES -
ID GRID-ID FX FY FXY MX MY MXY QX QY
0 16 CEN/4 0.0 0.0 0.0 7.416273E+02 2.897313E+02 -1.912638E+00 -2.195387E+01 -9.208935E+00
25 0.0 0.0 0.0 7.362260E+02 2.878116E+02 -1.912638E+00 -2.195387E+01 -9.208935E+00
8 0.0 0.0 0.0 7.362260E+02 2.916510E+02 -1.912638E+00 -2.195387E+01 -9.208935E+00
9 0.0 0.0 0.0 7.470287E+02 2.916510E+02 -1.912638E+00 -2.195387E+01 -9.208935E+00
10 0.0 0.0 0.0 7.470286E+02 2.878116E+02 -1.912638E+00 -2.195387E+01 -9.208935E+00 *** USER WARNING MESSAGE 6417 (SQD41)
THE (BILIN) OPTION FOR STRESSES IS NOT AVAILABLE FOR NONLINEAR MATERIAL OR COMPOSITE ELEMENTS.
USER INFORMATION: STRESS (CENTER) WILL BE APPLIED TO THOSE ELEMENTS.
User information:
CUBIC refers to corner output for element STRESS, STRAIN, and FORCE.
Corner output is not available for nonlinear analysis, so only center stresses are computed for nonlinear CQUAD4 elements. S T R E S S E S I N L A Y E R E D C O M P O S I T E E L E M E N T S ( Q U A D 4 )
ELEMENT PLY STRESSES IN FIBRE AND MATRIX DIRECTIONS INTER-LAMINAR STRESSES PRINCIPAL STRESSES (ZERO SHEAR) MAX
ID ID NORMAL-1 NORMAL-2 SHEAR-12 SHEAR XZ-MAT SHEAR YZ-MAT ANGLE MAJOR MINOR SHEAR
0 16 1 3.40298E+04 1.32944E+04 -8.77603E+01 -2.82061E+01 -1.18315E+01 -0.24 3.40301E+04 1.32940E+04 1.03681E+04
0 16 2 -2.87695E-10 -2.20519E-10 4.48237E-12 -2.82061E+01 -1.18315E+01 86.20 -2.20222E-10 -2.87992E-10 3.38853E-11
0 16 3 -3.40298E+04 -1.32944E+04 8.77603E+01 0.0 0.0 89.76 -1.32940E+04 -3.40301E+04 1.03681E+04 |
Repetimos "F5 > Deform > Contour > Deformed & Contour Data > Lam Ply1 XY Shear Stress" para representar las tensiones cortantes TAU-XY en la capa nº 1. En la barra de herramientas SELECT se recomienda activar el selector de entidad a Nodo y en el Modo de Selección activar "Show Tooltips", de esta forma al colocar el cursor encima del nodo#1 nos aparece en pantalla un cuadro con todos los resultados de desplazamientos y tensiones disponibles en ese nodo. Vemos que la tensión a cortadura TAU-XY en el punto "E" (nodo#1, elementos#1, 20, 36 y 64) tiene un valor de -5040 psi:
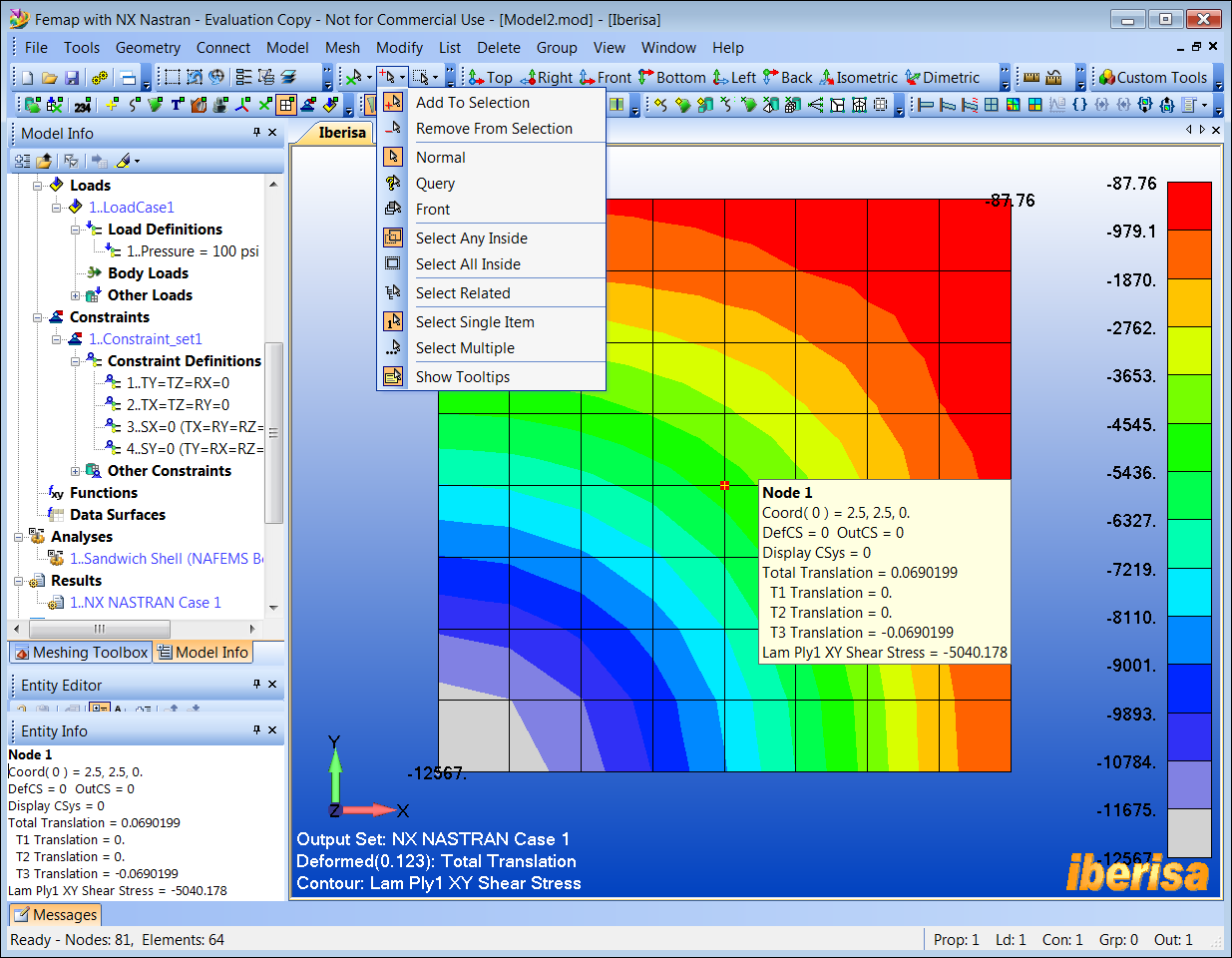
Resultados de Tensiones TAU-XY en el
Punto-"E"
15.
Comparación de Resultados
La siguiente tabla muestra los resultados de NX NASTRAN comparados con los
valores objetivo del NAFEMS Benchmark Test No. R0031/3 (Date Issue 17/12/98):
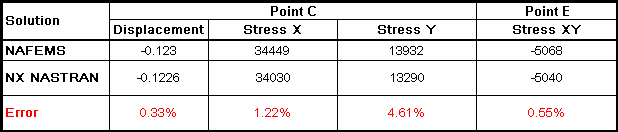
Tabla Comparativa de Resultados NX
Nastran vs. NAFEMS"
Espero que el tutorial os haya resultado útil e interesante!!.
Saludos,
Blas.
SÍGUENOS
EN: 
