FEMAP™
winLIFE está compuesto por los siguientes módulos (ver ejemplo de aplicación en mi BLOG trabajando con FEMAP y NX Nastran haciendo clic aquí.
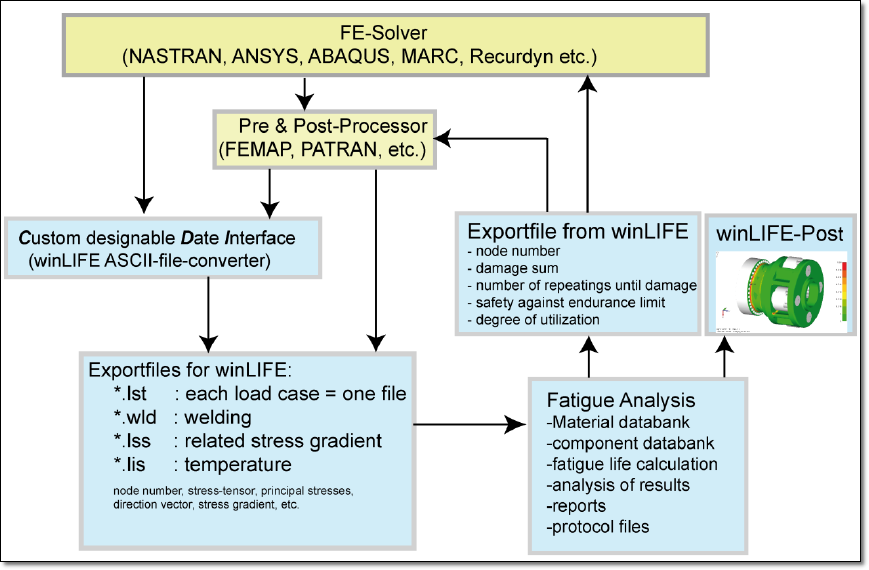
FEMAP™
winLIFE QUICK CHECK
Si las solicitaciones a las que se somete una pieza están muy por debajo del límite de fatiga, esta verificación puede realizarse de forma rápida y sin esfuerzo. No son necesarios más ensayos de resistencia a la fatiga. Sólo hace falta realizar un cálculo estático por Elementos Finitos aplicando la carga máxima y winLIFE QUICK-CHECK calcula el grado de utilización del límite de resistencia. Cualquier usuario de FEMAP puede aprender a usar winLIFE QUICK CHECK muy rápidamente.
• winLIFE BASIC
Permite realizar la estimación de vida a fatiga utilizando el Método Clásico basado en el cálculo a fatiga con tensión nominal uniaxial alterna (Nominal Stress Method), el método de tensiones locales (Elastic Notch Stress Method & S-N Curve), o el Método de Deformación Local (Local Strain Approach & ε-N Curve) utilizando factores de entalla de forma habitual para describir los efectos locales en la grieta.
• winLIFE MULTIAXIAL
Módulo adicional a winLIFE BASIC que se utiliza para calcular la vida a fatiga de piezas bajo cargas dinámicas con cambios considerables en la dirección de las tensiones principales.
• winLIFE MULTIAXIAL MULTI CORE
Tiene la misma funcionalidad que winLIFE MULTIAXIAL, pero permite aprovechar los múltiples CORES disponibles en la CPU del ordenador, obteniendo resultados de forma mucho más rápida.
• winLIFE GEARWHEELS & BEARINGS
Módulo adicional para calcular la vida a fatiga en dientes de engranajes y rodamientos.
• winLIFE CRACK PROPAGATION
El modulo CRACK PROPAGATION se basa en el Método de Tensión Nominal de acuerdo con la ecuación de Paris y Erdogan Ratwani.
• winLIFE RANDOM
Permite realizar análisis de fatiga en problemas de vibraciones bajo excitaciones aleatorias dadas por su PSD (Power Spectral Density). En la industria aeroespacial, naval, electrónica y ferroviaria se trata de un procedimiento de diseño muy común. Las pruebas experimentales tienen que ser realizadas por ensayo para la certificación de la estructura y con winLIFE RANDOM es posible dar una estimación de la vida a fatiga mediante cálculo por ordenador.
• winLIFE viewer4winLIFE
Este es un módulo adicional para winLIFE que permite representar los resultados gráficamente sobre el componente 3D. Simplifica el uso porque puede postprocesar resultados con un simple clic del ratón.
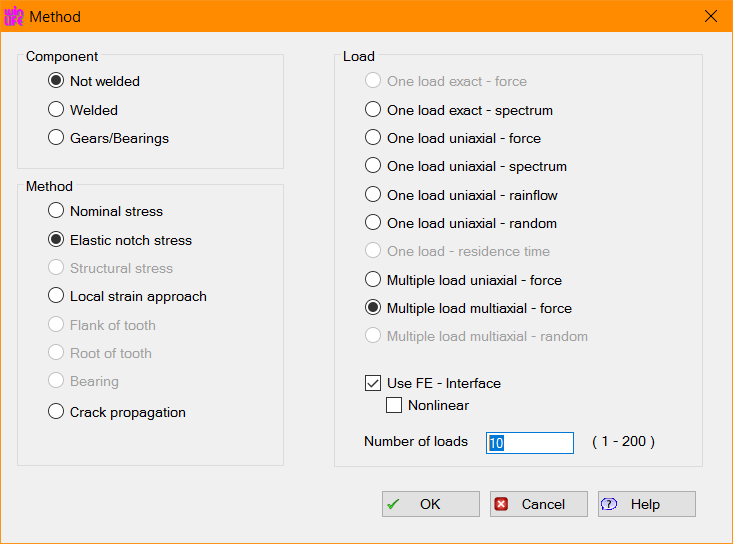
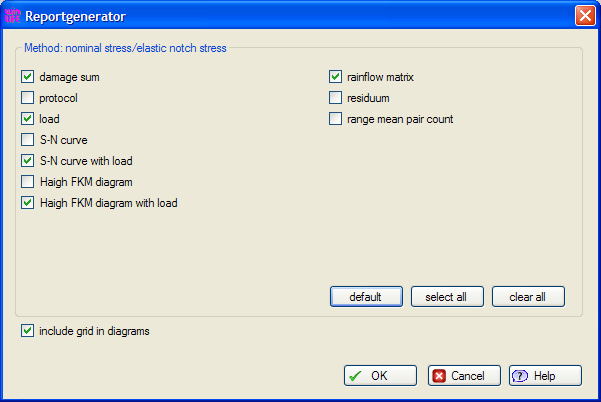
Windows nativo
winLIFE BASIC |
winLIFE MULTIAXIAL | winLIFE GEARWHEELS & BEARINGS |
| El cómputo de la vida a fatiga se puede realizar utilizando el Método Clásico basado en el cálculo a fatiga con tensión nominal uniaxial alterna (Nominal Stress Method), el método de tensiones locales (Elastic Notch Stress Method), o el Método de Deformación Local (Local Strain Approach) utilizando factores de entalla de forma habitual para describir los efectos locales en la grieta. | Módulo adicional al paquete básico que se utiliza para calcular la vida a fatiga de piezas bajo cargas dinámicas con cambios considerables en la dirección de las tensiones principales. | Módulo adicional para calcular la vida a fatiga en dientes de engranajes y rodamientos |
Métodos de Análisis de Fatiga en winLIFE
winLIFE soporta los métodos más importantes de análisis de vida a fatiga
| Nominal Stress Method | Elastic Notch Stress Method | Local Strain Approach |
|---|---|---|---|
Life-Curve: |
|
|
|
Achieving life curve: |
|
|
|
Fatigue life calculation |
|
|
|
Mechanical sizes taken into account: |
|
|
|
Limitations of the method: |
|
|
|
Combination with Finite Elements: |
|
|
|
Experience and advantages of the results: |
|
|
|
SOLVER Independiente
Los métodos basados en la curva S-N son los menos exactos, especialmente para fatiga de ciclos bajos. Pero son los más tradicionales, debido a que es sencillo de implementar para un amplio rango de problemas de diseño, y representa de forma adecuada los problemas de ciclos altos.
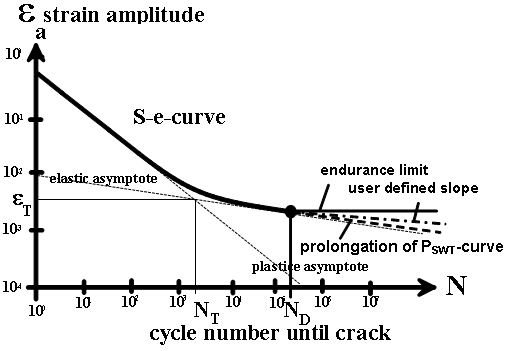
El método Local Strain Approach es más elavorado y requiere un análisis más detallado de la deformación plástica en regiones donde consideren las tensiones y deformaciones para estimación de vida a fatiga. Este método es especialmente recomendado para cálculo de fatiga de ciclos bajos. En este caso los datos de vida a fatiga a introducir en winLIFE consisten puramente en datos de materiales:
| Curva cíclica de Tensión-Deformación. | |
| Curva ε-N de deformación vs. nº de ciclos | |
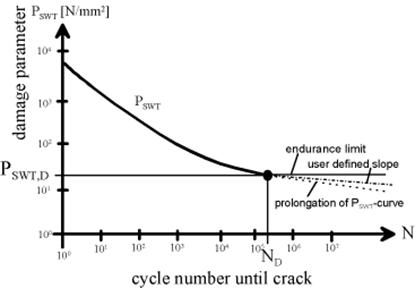
| Curva de parámetro de daño vs. nº de ciclos para considerar la sensibilidad a la tensión media. Hay gran cantidad de parámetros de daño diferentes, el más conocido es el PSWT según Smith-Watson-Topper. |
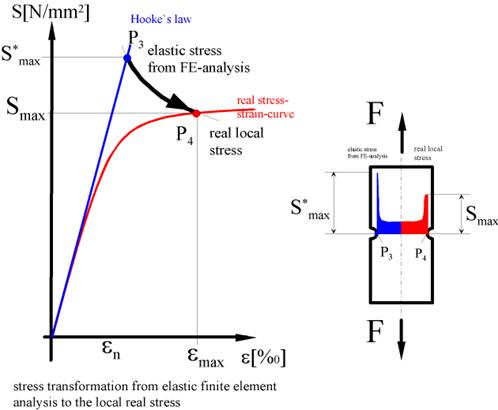
Al contrario del Nominal Stress Method el <método Local Strain Approach requiere conocer las tensiones y deformaciones reales en la zona de interés. Este dato puede ser calculado por el Método de los Elementos Finitos mediante un análisis elástico de tensión-deformación realizando una transformación a tensiones reales mediante la regla de Neuber.
El uso del método Local Strain Approach tiene las siguientes ventajas e inconvenientes:
Es posible utilizar un procedimiento automático en combinación con el Método de Análisis por Elementos Finitos lo que significa que el usuario no debe buscar el punto crítico. | |
Los datos para describir la vida a fatiga son puros datos del material. Esto resulta en un uso más universal del método. | |
Incluye el comportamiento real de tensión-deformación del material, por tanto las tensiones plásticas se modelizan correctamente. |
Una desventaja del método Local Strain Approach es que la teoría es mucho más compleja y los resultados son más difíciles de seguir para el usuario. Este problema es, sin embargo, contrarestado por el hecho de que winLIFE le da al usuario un gran soporte proporcionando resultados parciales para ayudarle a entender el procedimiento de cálculo.
Otra desventaja es una ley de material más compleja, pero debido a que las curvas de material son puros datos de material y pueden usarse de forma universal, el método Local Strain Approach es el método más conveniente.
Debido a una mayor experiencia en el Nominal Stress Method, en muchos casos puede ser una buena idea usar ambos métodos. Las difrencias en los resultados ayudará a hacer un análisis crítico de los parámetros utilizados y finalmente obtener una idea del rango de dispersión de los resultados obtenidos.
Análisis de Fatiga en Soldaduras con winLIFE
Las uniones soldadas son una fuente importante de reducción de la resistencia a fatiga debido a las tensiones residuales, a posibles fallos de llenado, poros, defectos, y concentración de tensiones. Para realizar un análisis de fatiga en estructuras soldadas existen numerosos procedimientos. Aquí vamos a presentar únicamente las ideas básicas debido a la existencia de diferentes normativas [FKM & Lloyd, GL(Ship), GL(Wind Energy)]. winLIFE permite realizar análisis de fatiga en soldaduras con prácticamente todas las normativas existentes.
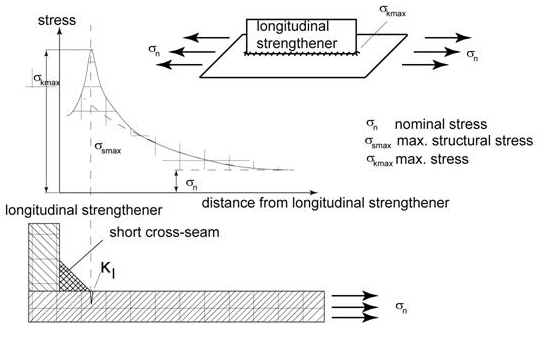
Para ver los diferentes procedimientos disponibles y explicar los diferentes tipos de tensiones usadas para el cálculo de fatiga utilizaremos el ejemplo de una placa base rigidizada longitudinalmente. La siguiente figura muestra las tensiones en el punto frontal del rigidizador.
Existen tres tipos de tensiones que se utilizarán en winLIFE para la predicción de vida a fatiga:
sn: tensión nominal en la placa base. Para usar esta tensión en la predicción de fatiga la información sobre la soldadura debe venir de una curva S-N. | |
skmax: máxima tensión en la entalla. Depende del nivel de detalle de la malla en la soldadura y existirá una gran dispersión de datos entre distintas soldaduras. | |
ssmax: máxima tensión estructural. Es la tensión obtenida por extrapolación entre dos (o tres) puntos. La dispersión es limitada comparada con la tensión máxima de entalla y es un método válido para el cálculo de fatiga en soldaduras. |
La siguiente tabla muestra los tres tipos de cálculo de soldaduras y sus características mostrando qué propiedad a considerar en cada procedimiento:
| Cálculo de Fatiga usando | Tensión Nominal (sn) | Tensión Estructural (ssmax) | Tensión de Entalla (skmax) |
|---|---|---|---|
| ¿Se considera en la tensión? | |||
| Component shape | No | Sí | Sí |
| Welding shape | No | Sí | Sí |
| ¿Se considera en la resistencia? | |||
| Component shape | Sí | No | No |
| Welding shape | Sí | Sí | No |
| Welding | Sí | Sí | Sí |
Reglas para utilizar la Máxima Tensión Estructural en Soldaduras
En los inicios Haibach propuso usar galgas extensométricas (strain gauges) en frente de las soldaduras y usar las mediciones de deformaciones unitarias bajo cargas de servicio para realizar predicciones de vida a fatiga. Estableció reglas sobre dónde y cómo colocar las galgas de medición y demostró que se pueden obtener resultados fiables.
Esta idea se puede transferir perfectamente a los cálculos por elementos finitos. De forma similar a las galgas extensométricas, los resultados en los «puntos de medición» se usan para extrapolar las tensiones.
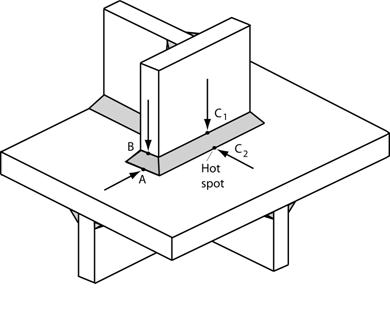
La posición de los puntos de referencia depende del tipo de estructura. La siguiente figura muestra una placa con tres tipos de puntos críticos a fatiga (tipos A, B y C) propuesta por Fricke (Recommended hot spot analysis procedure for structural details of ships and FPSOs based on round-robin FE analyses, Int J Offshore Polar Engng, 20020 12 [1], 40-47):
- Weld-toes at the end of an attachment
- Weld-toes on the plate edge at the end of an attachments
- Weld toes on the plate surface amid the weld along an attachment
La posición de las galgas depende del espesor de las placas «t«. La tensión estructural se obtiene por extrapolación (lineal o no lineal) de la tensión en el borde de la soldadura (weld toe). La siguiente figura muestra que se puede usar una extrapolación lineal o no lineal [casos a) y b)] para los tipos de soldaduras A y C. El tipo de soldadura B requiere una extrapolación según el caso c).
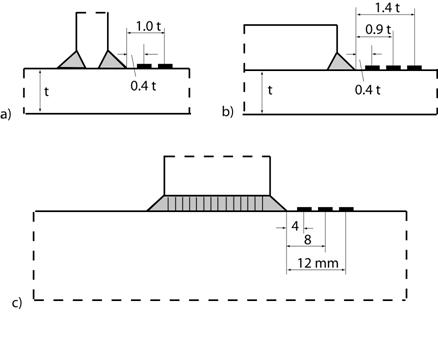
Este procedimiento se puede realizar usando los resultados de tensión a partir de un cálculo de elementos finitos. La estructura real se malla con elementos Shell o Sólidos [elementos CQUAD4 o CEHEXA(8) en NX Nastran]. El tamaño del elemento irá en función del espesor de la placa para crear un modelo de elementos finitos con un tamaño del modelo en nodos y elementos limitado. Las flechas de la figura, incluyendo los círculos, muestran los puntos en donde se leerán las tensiones de referencia (reemplazando las galgas). La extrapolación al borde de la soldadura (weld toe) en el modelo mallado con elementos sólidos [caso b)] o a la intersección entre planos en el modelo mallado con elementos Shell [caso a)] debe realizarse por el usuario. Esta labor se realiza mediante una macro en FEMAP, el pre-procesador de elementos finitos del solver NX Nastran.
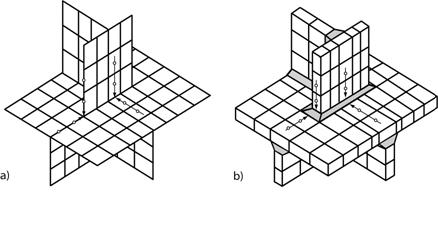
En modelos basados en elementos Shell la soldadura en general no se modeliza y la malla (nodos y elementos) se coloca en la superficie media de las placas. Unicamente si los cordones de soldadura están situados de forma excéntrica entonces se puede considerar modelizar la soldadura. La siguiente figura muestra algunos ejemplos de mallado de la soldadura en modelos Shell.
El caso a) muestra dos modelos, en la figura superior no se considera meter en el modelo la soldadura mientras que en la figura inferior se malla la soldadura, en ambos casos se utilizan elementos rígidos RBE2 para unir las placas soldadas. | |
En el caso b) debido a una posición excéntrica del cordón de soldadura se malla la soldadura con un elemento Shell al que se le asigna un espesor equivalente a la dimensión de la garganta de la soldadura. |
El objetivo principal es capturar y tener en cuenta el cambio de rigidez de la estructura y ver la influencia del cordón de soldadura para tomar la decisión de considerar o no el mallado de forma explícita del cordón de soldadura en el modelo de elementos finitos.
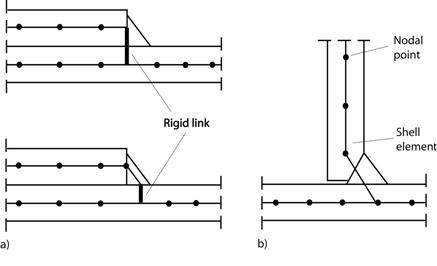
Modelado de soldaduras excéntricas en modelos de EF mallados con elementos Shell:
a) Unión entre placas paralelas
b) Unión entre placas en T
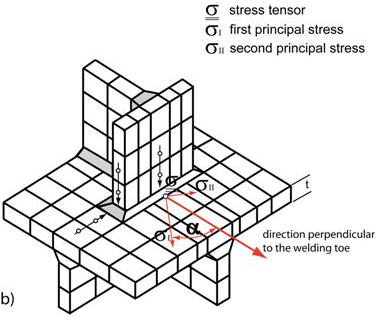
En el caso de carga proporcional (con pequeños cambios en la dirección de las tensiones principales) se recomienda utilizar el valor de la máxima tensión principal como el parámetro de daño. Para calcular la tensión en el borde de la soldadura se deben conocer las distancias a los puntos de referencia. En estos puntos de referencia P1 y P2 se necesitará conocer los tensores de tensión SP1,i y SP2,i para cada instante de tiempo:
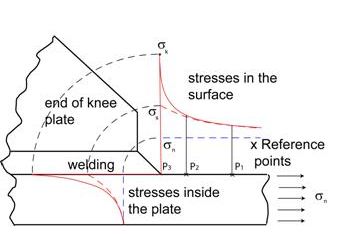
La siguiente figura muestra el reparto de tensiones en una pieza soldada, donde el Punto P3 representa el borde de soldadura en el cual se desea calcular la vida a fatiga de la pieza. Los Puntos P1 y P2 están situados en la superficie a una distancia de 0.5 t y 1.5 t respectivamente, perpendicular al borde de la soldadura. Un vector unitario n perpendicular al borde de la soldadura también es necesario.
Modelado de soldaduras excéntricas en modelos de EF mallados con elementos Shell:
a) Unión entre placas paralelas
b) Unión entre placas en T
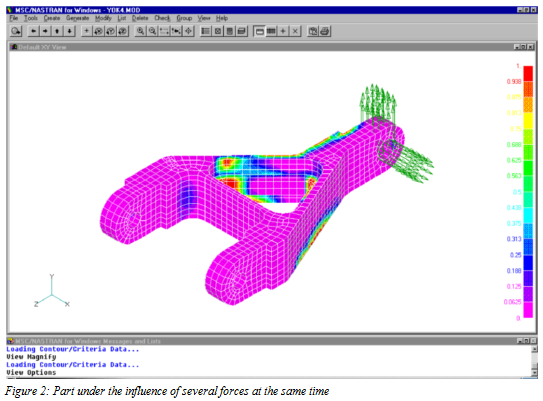
Ejemplos de Aplicación de winLIFE
La siguiente figura muestra un ejemplo de una pieza de dirección bajo cargas dinámicas. Está cargada mediante fuerzas verticales y horizontales F1 y F2 . Debido a que las fuerzas no son proporcionales, existirá un gran cambio en la dirección de las tensiones principales. Este problema se considera un caso de Fatiga Multiaxial.
